Gas Behavior

The content that follows is the substance of lecture 20. In this lecture we cover the Gas Laws: Partial Pressures, Kinetic Molecular Theory and Real Gases.

Partial Pressures:

Dalton’s Law of Partial Pressures: The total pressure exerted by a mixture of gases is the sum of their individual partial pressures.

P_total = P₁ + P₂ + P₃ + …..

There are two ways to calculate partial pressures:

Example 1:

A 1.00 L sample of dry air at 25.0 ^oC contains 0.319 mol N₂, 0.00856 mol O₂, 0.000381 mol Ar, and 0.00002 mol CO₂.  Calculate the partial pressure of N₂(g) in the mixture.

At first this looks really intimidating with all of the moles given for each gas but if you read the question carefully you realize that it just wants the pressure for nitrogen and you can calculate that very simply by use of the ideal gas law:

p = nRT/V = 0.319 mol(0.08206 L.atm/mol/K)(298.15K)/1.00L = 7.80 atm

Example 2: 

A sample of intestinal gas was collected and found to consist of 44% CO₂, 38% H₂, 17% N₂, 1.3% O₂ and 0.0030% CH₄, by volume. (The percentages do not total 100% because of rounding)  What is the partial pressure of each gas if the total pressure in the intestine is 818 Torr?

For this question we need to remember that the total pressure is the total of each partial pressure and the partial pressure is equal to the mole fraction X of each gas times the total pressure.

PP = XP_Total

First we need to calculate the moles of each of the gases in the mixture. If we assume 100 grams, we can multiply the percentages given and use the resulting gram amounts to calculate each of the mole amounts:

44% x 100 g = 44g CO₂ x (1 mol CO₂/44.0g CO₂)= 1 mol CO₂

38% H₂ x 100 g = 38 g H₂ x (1 mol H₂/2.0g H₂)= 19 mol H₂

17% N₂ x 100 g = 17 g N₂ x (1 mol N₂ /28 g N₂)= 0.61 mol N₂

1.3% O₂ x 100 g = 1.3g O₂ x (1 mol O₂/32g O₂)= 0.041 mol O₂

0.003% CH₄ x 100g = 0.003g CH₄ x (1 mol CH₄/16 g CH₄)= 0.00019 mol CH₄

Total Moles all gases = 1mol + 19 mol + 0.61 mol + 0.041 mol + 0.00019 mol = 20.6529 mol

Mole Fraction = mol gas/mol total

So calculating the mole fraction and then multiplying the fraction by the total pressure will give the partial pressure of each:

1 mol CO₂/20.6529 mol x 818 Torr = 40. Torr

19 mol H₂/20.6529 mol x 818 Torr = 750 Torr

0.61 mol N₂ /20.6529 mol x 818 Torr = 24 Torr

0.041 mol O₂/20.6529 mol x 818 Torr = 1.6 Torr

0.00019 mol CH₄/20.6529 mol x 818 Torr = 0.0075 Torr

The pressures don't add up to 818 Torr exactly due to rounding but they should be close.

Partial Pressure Practice:

 

 

---

Kinetic Molecular Theory

The Kinetic Molecular Theory describes the relationship between the motion of gas particles and their properties. The theory makes several assumptions:

 

Pressure – Assessing Collision Forces

The force of the impacts experienced by the walls of a container is what we use to determine the pressure of a gas.

•Translational kinetic energy
•Frequency of collisions
•Impulse or momentum transfer
•Pressure proportional to impulse times frequency

 

While these equations can look intimidating what they are really saying is that the pressure of a gas is simply proportional to the frequency and force with which the molecules are striking the container walls.

Pressure and Molecular Speed

Assume 1 mole in 3 dimensions (E.G. 1/3)   PV = nRT so   NA * m = M (molar mass)   Then Rearrange to get the Root Mean Squared Speed of the gas

 

The derivation of the equation shown above also looks intimidating but the end result just says that the speed at which a gas travels is inversely proportional to the square root of its molar mass (M) or that bigger gases travel slower.

Speed and Temperature:

Using the equations above and substituting the Ideal Gas Law and definition for kinetic energy (e_K) into the equation for one mole:

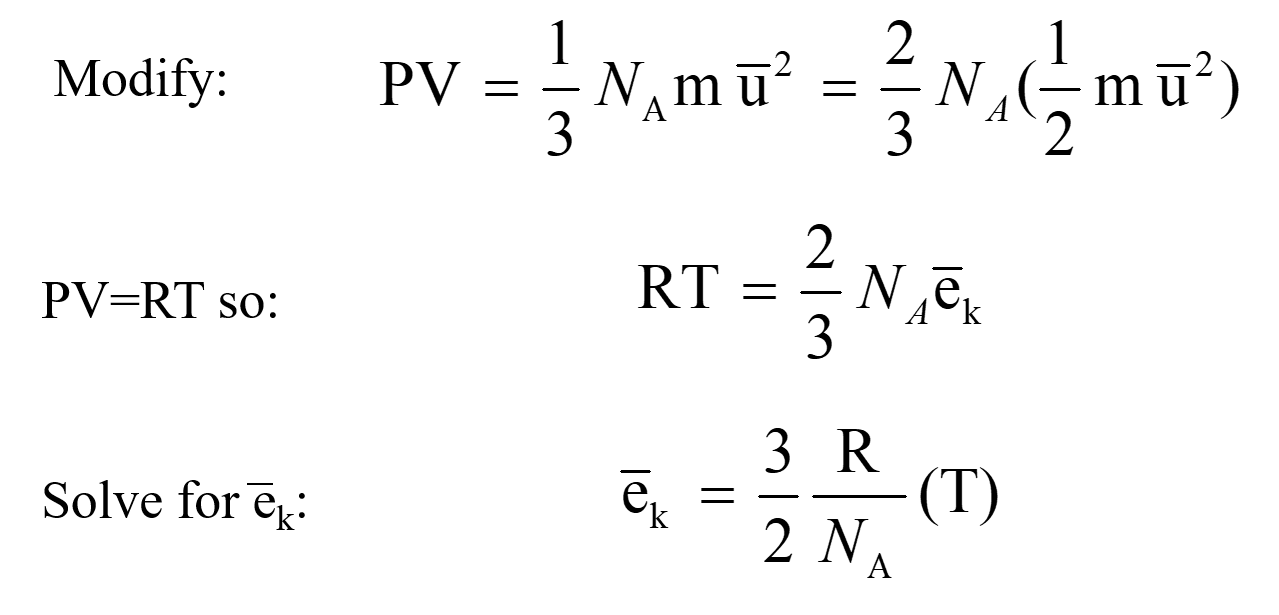
We can see from the final equation that the relationship between the kinetic energy of a gas and temperature is one of direct proportionality.

Diffusion and Effusion:

Two properties of a gas which derive directly from the relationships shown above are those of Diffusion and Effusion.

(a) Depicts the process of Diffusion = the mixing process of two or more gases (b) Depicts the process of Effusion = the process of a gas escaping from a container through a small hole.

In both cases, the net speed at which the process occurs is proportional to the molar mass of the gas(es) involved:

The equation above is called Graham's Law of Effusion and is named after the scientist that derived it. The conditions under which the law can be applied are as follows:

The law can be used to make a number of calculations:

Here are some practice problems for you to try: Questions and Answers

Real Gases

Up to this point we have been discussing the gases studied as Ideal. That is to say they obey the Ideal Gas Law. The reality is that very few gases obey this law except at very high temperatures or low pressures. Most gases act like Real Gases at room temperatures and pressures and this means they have a different set of properties that have to be considered when you try to calculate their pressures or volumes. Here are the differences that you should know:

Because of the small but non-zero interactions and volumes of a real gas, the ideal gas law must be amended to consider these factors.

Volume Correction

In an Ideal gas we neglected the volume of the gas so no matter what the identity of the gas or how many molecules were present in a space we assumed the distance between them was the same. But in a real gas, the size of the molecule of gas DOES MATTER. The actual volume free to move in is less because of particle size and more molecules will have more effect.

The correction to the volume is there for the number of moles (n) of the gas times a constant (b) subtracted from the Ideal Gas volume where the value of b is individual to the identity of the gas.

Pressure Correction

Because in a Real gas the molecules do have some interaction/attraction, the pressure observed will be less than that of an ideal gas. The correction must take into account both the concentration of the gas (n/V) as well as the attraction between the two gases (n/V)² and again this factor must be individualized to the gas by a constant a. The entire correction is shown below:

Substitution of these two corrections for pressure and volume into the normal Ideal Gas Law yields the Van der Waal's Equation:

Where the values of a and b are determined by experiment, and are different for each gas. The values of b will be larger for larger molecules of gas and since the interactions of the gas will depend on its attractive properties like polarity (unequal distribution of electrons throughout the molecule causes partial positive and negative areas that can be more attractive to molecules of opposite charges distributions), the values for a will increase with both size and polarity.

For our purposes, the calculation of this equation would be more of an exercise of mathematical skills rather than an understanding of the chemistry so I will not be presenting an example calculation here nor will put one on a test BUT I do expect you to know the differences between the properties of an Ideal versus Real Gas and how those differences are dealt with in the equation above.