Quantum Theory
The content that follows is the substance of General Chemistry Lecture 25. In this lecture we continue the discussion of electromagnetic Radiation and introduce Bohr's Theory of the Atom and the Quantum Numbers.
Electromagnetic Radiation Continued
The electromagnetic Radiation we observe comes from the change in location of electrons in the atoms of different elements. What we need to discuss is how those electrons are used to produce the different wavelengths of light and what we mean when we say that light is "quantized". Bohr's Theory shows that the electrons around a nucleus are not randomly distributed but rather exist in specific energy levels called "shells" and it is the movement of the electrons between these shells that causes the emission or absorption of energy and thereby the emission or absorption of light. |
 |

Bohr's Model
The Bohr model consists of four principles:
1) Electrons assume only certain orbits around the nucleus. These orbits are stable and called "stationary" orbits.
2) Each orbit has an energy associated with it. For example the orbit closest to the nucleus has an energy E1, the next closest E2 and so on.
3) Light is emitted when an electron jumps from a higher orbit to a lower orbit and absorbed when it jumps from a lower to higher orbit.
4) The energy and frequency of light emitted or absorbed is given by the difference between the two orbit energies, e.g.,
ΔE(light) = EF - EI
If the orbits of the electron are restricted, the energies that the electron can possess are likewise restricted and are defined by the equation:

Where RH is a constant called the Rydberg constant and has the value
2.18 x 10-18 J
Note this value is a combination of a Rydberg constant 1.097 × 107 m–1 * Planck's Constant and the Speed of Light. (RH*h*c)
'n' is an integer, called the principle quantum number and corresponds to the different allowed orbits for the electron. Thus, an electron in the first allowed orbit (closest to the nucleus) has n=1, an electron in the next allowed orbit further from the nuclei has n=2, and so on.
Thus, the relative energies of these allowed orbits for the electrons can be diagrammed as follows:

All the relative energies are negative
Points to Note:
•The lower the energy, the more stable the atom
•The lowest energy state (n=1) is called the ground state of the atom
•When an electron is in a higher (less negative) energy orbit (i.e. n=2 or higher) the atom is said to be in an excited state
•As n becomes larger, we reach a point at which the electron is completely separated from the nucleus
·E = (-2.18 x 10-18 J)(1/infinity) = 0
·Thus, the state in which the electron is separated from the nucleus is the reference or zero energy state (actually higher in energy than other states)
Bohr also assumed that the electron can change from one allowed orbit to another:
•Energy must be absorbed for an electron to move to a higher state (one with a higher n value)
•Energy is emitted when the electron moves to an orbit of lower energy (one with a lower n value)
•The overall change in energy associated with "orbit jumping" is the difference in energy levels between the ending (final) and initial orbits:
ΔE(light) = EF - EI
Substituting in for the previously defined energy equation:
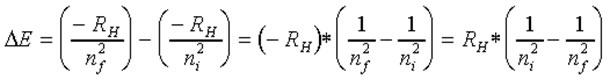
When an electron "falls" from a higher orbit to a lower one the energy difference is a defined amount and results in emitted electromagnetic radiation of a defined energy (ΔE)
Remember that Planck had deduced that the energy of the photons comprising EM radiation is a function of its frequency (E = hv)
Therefore, if the emitted radiation from a falling electron had a defined energy, then it must have a correspondingly defined frequency :
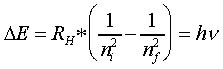
Note:
ΔE is positive when nf is greater than ni, this occurs when energy is absorbed and an electron moves up to a higher energy level (i.e. orbit). When ΔE is negative, radiant energy is emitted and an electron has fallen down to a lower energy state. Note that if you are solving for n in a question you may need to SET the sign of the hv as negative if the process is an emission to get the correct value of n.

Here is an example use of this equation:
Here are some practice problems:
De Broglie’s Equation
In 1924 a young physicist, de Broglie, speculated that nature did not single out light as being the only matter which exhibits a wave-particle duality. He proposed that ordinary "particles'' such as electrons, protons, or bowling balls could also exhibit wave characteristics in certain circumstances. Quantitatively, he associated a wavelength to a particle of mass m moving at speed v :
λ = h / mv
h = Planck’s constant
m = the mass of the object
v = the velocity of the object
Here are some practice problems
Organizing the Electrons around an Atom: The Quantum Numbers
Starting with some rules, the Pauli Exclusion Principle states that no two electrons can have the
same set of four quantum numbers.
There are 4 quantum numbers designed to describe the location of an electron in an atom:
n = The Principle Quantum Number
l = Azimuthal Quantum Number
ml = Magnetic Quantum Number
ms = Spin Quantum Number
n The Principle Quantum Number
1)Can be any whole number from 1 - ∞
2)measures the average distance of the e- from the nucleus
3)different values of n mean different energy levels
4)different values of n mean relatively large differences in the energies of the e-s
5)the smallest average distance and the lowest energy occurs when n = 1; each increase in n increases those quantities.
6)the number of e- possible in a level is 2n2
l The Azimuthal Quantum Number
1) l goes from 0 to n-1 within an energy level
2) l values = 0 (for s), 1(for p), 2 (for d), 3 (for f) sublevels
3) indicates the shape of the orbital ( set of probable locations of the e- )
4) diff. values of l mean diff sublevels. In a sublevel all the e- have nearly the same energy.
5) different sublevels within the same level may have moderately large differences in energy.
6) within any level, the lowest energy sublevel is s, then p, then d, then f.
7) the number of possible values of l for a level is equal to the value of n
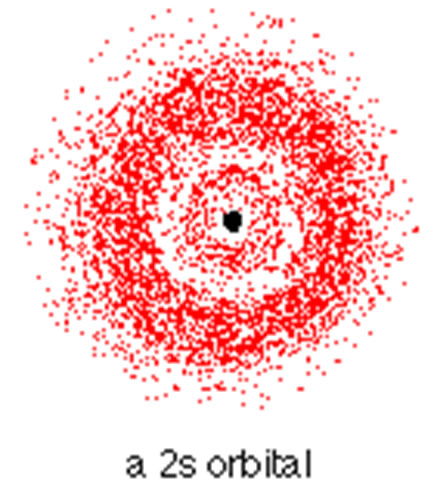
S Orbitals
1)all s orbitals have l = m = 0, the value of n can vary 2)95% of the time the electron will be found within a fairly easily defined region of space quite close to the nucleus. Such a region of space is called an orbital. 3)The space between orbitals is called a node. 4)Orbitals are areas where there is a high probability of finding an electron. |
 |
P Orbitals
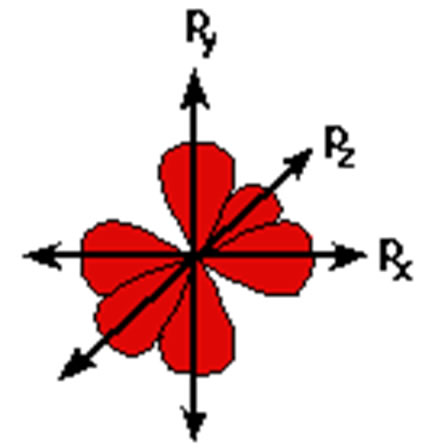 |
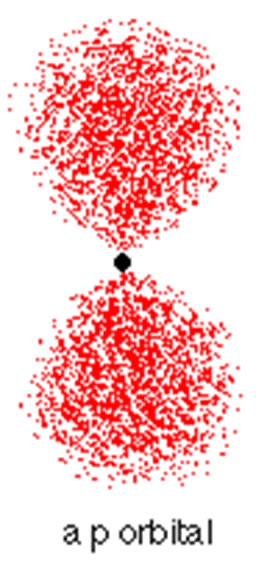 |
d Orbitals
There are 5 d orbitals
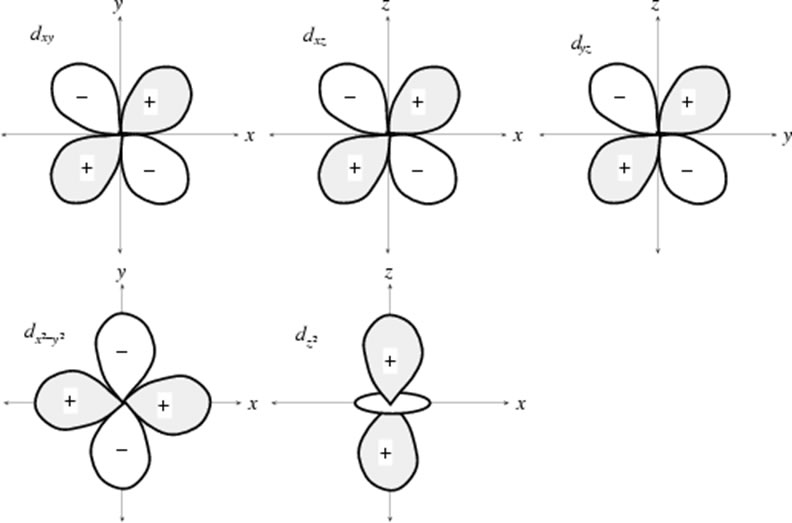
f Orbitals
There are 7 f orbitals
ml Magnetic Quantum Number
1)Values of ml go from +l to - l , which gives 2l + 1 number of values
2)identifies the direction the e- orbital has around the nucleus
3)specifies the e- orbital in which the e- is located within a sublevel.
4)different values of ml mean little difference in energies of the e-
5)the number of possible values of ml within a sublevel idenities how many e- pairs that the sublevel can hold
ms Spin Quantum Number
1)has 2 values:
+1/2 (spin up) and -1/2(spin down
2)identifies the "spin" or rotation of the e- about its own axis
3)shows that each orbital can contain only 2 e-
4)the direction of spin is either in one direction or the other
5)when 2 e- (in an atom) have the same set of QN except for ms, then these e- are called an e- pair
6)these e- within an e- pair have essentially the same energy
In Summary:
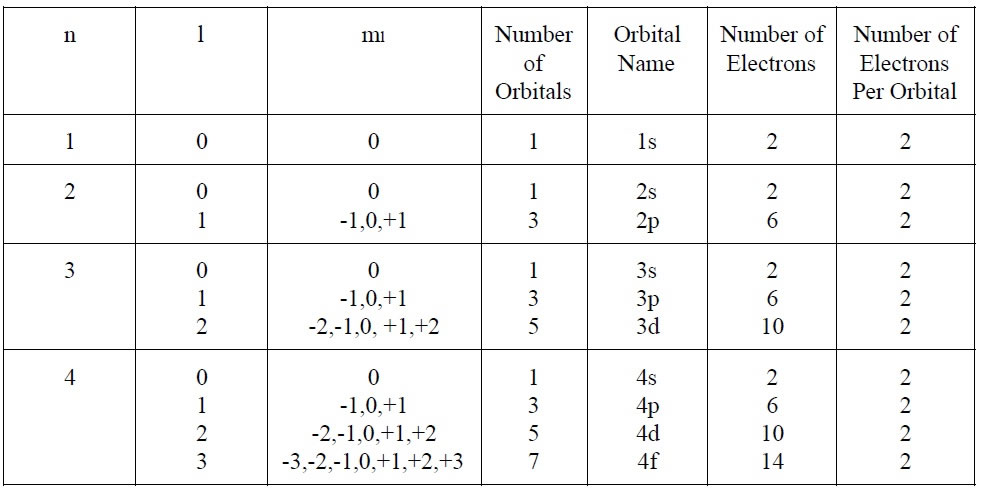
Let's Practice:
