
Background
Acid and Base Strength
The strength of an acid or base is determined by its ability to dissociate in water. An acid that completely dissociates to form its component ions H+ and A- when placed in water is a strong acid. The same can be said for a base that completely dissociates into B+ and OH-.
Acid and base strengths are characterized quantitatively by a value called the Ka and Kb (acid/base dissociation constants) respectively. These dissociation constants are calculated as a ratio of the amount of acid or base that is separated into ions over the amount of acid or base that is still together in acid or base form.
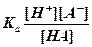 or or 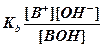
Therefore strong acids and bases will have Ka and Kb values greater than one since they are completely dissociated. Weak acids and bases have values less than one since the concentration of the acid or base that remains together will be greater than the concentration of the separated ions.
pH
In addition to the Ka or Kb indicating the strength of an acid or base, we often use the pH of the solution to describe whether a solution is acidic or basic. Solutions with a pH of less than 7 are considered acidic and solutions with a pH of greater than 7 are considered basic. Below are some more of the relations between acid and base concentration and pH:
pH = -log [H+] and [H+] = 10-pH
pOH = -log [OH-] and [OH-] = 10-pOH
pH + pOH = 14 and [H+]*[OH-] = Kw = 1 x 10-14
The determination of the pH and concentration of a weak acid or base solution is complicated by the less than 100% dissociation and will be discussed further in the second semester of this course. For now, we will only worry about calculating the concentration and pH of solutions containing strong acids and bases.
The pH of a strong acid solution is equal to the –log of the hydrogen ion concentration of that solution. Because the strong acid completely dissociates into ions, the acid concentration equals the hydrogen ion concentration.
For example: A 2.5M HCL solution has a [H+] = 2.5M and the pH = -log(2.5) = -0.40
The same relationship can be described for the pOH of a strong base. The hydroxide ion concentration will equal the concentration given for the strong base:
For Example: A 2.5 M NaOH solution has a [OH-] = 2.5M and the pOH = -log(2.5) = -0.40 So the pH = 14 –(-0.40) = 14.4
A couple of things should be noted about the examples above. First, students often think that pH values cannot be above 14 or below 0. As you can see from the examples given this is simply not true. When dealing with strong acids and bases the pH values are often very large or even negative. Second, you have to be careful when calculating the concentration of a base solution. The negative log of that solution gives you the pOH not the pH and students often forget this very important second calculation.
The Reaction of a Strong Acid with a Strong Base
In this experiment, the strong acid, HCl, and the strong base, NaOH, are used to create serial dilutions which are combined to form salt solutions of NaCl according to the reaction below:
HCl(aq) + NaOH(aq) à NaCl(aq) + H2O(l)
These products (a salt and water) are typical of the strong acid/base reaction and can be used to predict the products of other strong acid and base reactions.
Ex. H2SO4 + 2KOH à K2SO4 + 2H2O
Although the reactants have changed, the basic products remain the same: a salt and water.
Prediction of the amount of salt produced is based on the stoichiometry of the reaction and the amount of acid and base provided. In the case of HCl and NaOH, the reaction is “one-to-one” and therefore whichever reactant is present in the smallest amount of moles, it will limit the product moles that can be formed. This amount of moles will be the theoretical yield of the reaction. The actual yield will be determined experimentally.
Serial Dilutions
Serial dilution is an important technique in experimentation. The process allows the researcher to create controlled, systematic dilutions from a stock solution. Each successive solution is diluted so that the concentration of solute is changed by a desired ratio. For example, in 1/10 serial dilutions starting with a stock solution of 5M solute concentration, the serial dilution would be comprised of 5M, 0.5M, 0.05M, 0.005M… Each solution is reduced to one tenth of the previous solutions concentration. For another example, 1/25 serial dilutions starting from a stock solution of 12M solute concentration would be comprised of 12M, .48M, 0.0192M, 0.000768M… The greater the ratio of solute concentration change, the greater the difference in concentration for each successive serial dilution. Serial dilutions also work to conserve supplies since they use the previously made solution as the “stock” solution for the next more dilute solution.
For Example:
Using a 0.5M stock solution, create 4 solutions of 1/25 serial dilutions. Calculate the resulting concentration for each diluted solution using the following equation:
M1V1= M2V2
where M1 is concentration of solution one, V1 is the volume of solution one, M2 is concentration of solution two, and V2 is volume of solution two.
(1.0 mL)(0.5M) = (25 mL)(X)
X = 0.02 M
The results indicate that 0.02M is the concentration of the new diluted solution.
This process is repeated in order to make the next 1/25 diluted solution. But the stock solution used this time is the newly made 0.02M solution. Repeating the calculations above:
(1.0 mL)(0.02M) = (25 mL)(X)
X = 8.0 x 10-4M
The process continues using each newly made solution as the stock for the next lower concentration until all of the dilutions needed are produced.
As you can see, making 1/25 dilutions very rapidly drops the H+ concentration to very small amounts quickly. At some point, the concentration of the acid will actually fall below the concentration of H+ found in pure water. (The pH of pure water is 7 so the [H+] = 1.0 x 10-7M) Once you get to this point you must take into consideration not only the ions from your dilute acid but those from the water dissociation as well.
From the charge balance relationship [H+] = [Cl-] + [OH-], you can substitute for [OH-] from the water ionizatiion constant:
[H+] = [Cl-] + Kw/[H+],
and on rearrangment you get the quadratic equation:
[H+]2 - [Cl-][H+] - Kw = 0
This equation can be solved for [H+] using the quadratic formula. |