
Background
In studying chemical processes, attention is usually centered upon the properties of the substances involved. However, energy changes due to changes in the state of the system are associated with these processes. A system is that region of the universe under consideration. The surroundings are everything other than the system. Thus, the state of the system is specified by a number of variables, including temperature, pressure, volume, and chemical composition. A more extensive discussion of these energy relationships can be found in your textbook.
When a system undergoes any chemical or physical changes, the First Law of Thermodynamics requires that the accompanying change in the system’s internal energy (DE) is equal to heat (q) plus work (w):
 Equation 1 Equation 1
Thus the energy of a system increases when heat is added (q is positive) and/or work is done on the system (w is positive). For systems under constant pressure (note subscript p), Equation 1 becomes:
 Equation 2 Equation 2
The value for the heat (per mole) absorbed or given off by a system at constant pressure (qp) is called the heat of reaction or enthalpy of reaction (DH). By substituting DH for qp and rearranging, Equation 2 becomes:
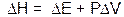 Equation 3 Equation 3
If there is no change in volume (no DV), then DH is the change in energy of the system at constant pressure. Therefore, DH is a useful quantity to measure for reactions in solution (at constant pressure) where no gaseous products are formed (no change in volume). This describes a lot of chemistry. (Note: Although one of the reactions we are using in this experiment does produce a gas, the change in volume is negligible. So we will maintain our assumption of constant volume. But as with all assumptions, we should acknowledge it as a possible source of error in the conclusion.)
The amount of heat (q) necessary to raise the temperature of a system is an extensive property. That is, it depends on the amount of material, as well as what the material is and how much the temperature changes. This can be expressed in two ways:
 Equation 4 Equation 4
where n is the number of moles of material, Cm is the molar heat capacity and DT is the change in temperature (either in K or °C; since it’s a change, it doesn’t matter). Alternatively, this can be expressed for the mass of the material as:
 Equation 5 Equation 5
where m is the mass of the material in grams, cp is called the specific heat of the material and DT is the change in the temperature (either in K or °C). If the conditions are restricted to constant pressure, these expressions become:

The formal definitions of the constants described above are: Molar heat capacity (Cm) is the amount of heat required to raise the temperature of one mole of material by one degree Kelvin or Celsius. Specific heat (c) is the amount of heat required to raise the temperature of one gram of material by one degree Kelvin or Celsius. The value of Cm or cp depends on the identity of the material, its state (gas, liquid, solid), and its temperature. Below is a table of the values these “constants” take on for various states and temperatures of water. Note that for most of the large range of liquid water temperatures, the value does remain fairly constant (to two significant figures).
Table 1. Molar Heat Capacities and Specific Heats for Water
State |
Temperature (ºC) |
Temperature (K) |
Heat Capacity
(J/mol * K) |
Specific Heat
(J/g * K) |
Specific Heat
(cal/g * K) |
Solid |
-34.0 |
239.2 |
33.30 |
1.846 |
0.4416 |
Solid |
-2.0 |
271.2 |
37.78 |
2.100 |
0.5024 |
Liquid |
0.0 |
273.2 |
75.86 |
4.218 |
1.007 |
Liquid |
25.0 |
298.2 |
75.23 |
4.180 |
0.9983 |
Liquid |
100.0 |
373.2 |
75.90 |
4.216 |
1.007 |
Gas |
110.0 |
383.2 |
36.28 |
2.01 |
0.481 |
An older (English system) unit used to express heat is the calorie. It is defined as the amount of heat necessary to raise 1 gram of water from 14.58°C to 15.58°C at one atmosphere pressure. Obviously, since much work is done in aqueous solutions, this is still a useful unit, even though it is not an SI unit. (Note: The food Calorie, abbreviated Cal, is actually 1000 calories or one kilocalorie.)
In order to determine the state function, enthalpy (DH), the heat (qP) of a particular reaction is divided by the number of moles of material involved in the reaction.
 Equation 6 Equation 6
The Calorimeter Cup
The term calorimetry refers to the measurement of heat released or absorbed during a chemical or physical process. The ideal calorimeter is well insulated so that its contents do not gain or lose heat to the surroundings, and is constructed of a material of low heat capacity so that only a small amount of heat is exchanged between the contents and the calorimeter. For many processes a simple, unsealed, insulated cup can be used as a calorimeter since it has a low heat capacity and excellent insulating properties. Constant pressure on the reaction is maintained by the atmosphere.
In reality, no calorimeter is ideal. Thus, to obtain reliable results the calorimeter must be calibrated to determine how much heat is exchanged with the calorimeter cup (and/or other surroundings). This correction factor is called the calorimeter constant (heat capacity of the calorimeter in J/K) and fits into an equation similar to the ones above. The temperature change of the cup can be assumed to be the same as that of the solution in it. Since the DT of the cup will change with each experiment, it is useful to have a calorimeter constant which can be used in all experiments as follows:
 Equation 7 Equation 7
The heat capacity of the calorimeter cup (Ccup) is determined by performing a separate experiment in which no chemical reaction takes place. Instead, hot water is added to the cold water in the calorimeter. The amount of heat lost by the hot water (qhw) must be equal to the heat gained by the cold water (qcw) plus the heat gained by the calorimeter cup (qcal). (We can’t lose energy, so it only has two places to go.) This can be written as:
 Equation 8 Equation 8
Note that the signs of these amounts of heat are opposite because the hot water is losing energy and the cold water and cup are gaining energy.
The amount of heat (qcal) absorbed by the cup is easily found, since qhw and qcw can be calculated using Equation 5. To determine qhw, substitute the mass of the hot water, the specific heat of water (Table 1), and the temperature change for the hot water (DT) into the equation. The qcw is found the same way. Once qcal is found, Ccup can be calculated from Equation 7.
To clarify the principles of calorimetry, consider the following hypothetical experiment. Using calorimetry methods, a determination of the heat of reaction of NaOH in HCl is made.

The heat capacity for the calorimeter cup is given as 6.80 J/K. In the experiment, 75 mL (75 g, assume a density of 1.0 g/mL) of a 0.6 M HCl solution is placed in the calorimeter and allowed to equilibrate to room temperature. Then 75 mL (75 g) of a 0.6 M NaOH is added to the calorimeter with stirring. Temperature readings are taken before and after addition of the NaOH for 10 minutes. Plotting temperature vs. time gives the following plot.
Time (sec)
|
Temp. (ºC) |
0 |
22.8 |
30 |
22.8 |
60 |
22.9 |
90 |
23.6 |
120 |
28.2 |
150 |
27.8 |
180 |
27 |
210 |
26 |
240 |
25.5 |
270 |
24.8 |
300 |
24.1 |
330 |
23.7 |
360 |
23.6 |
Temperature vs. Time

Note that this is a cooling curve, and the data of interest is on the left of the graph. The initial temperature (Ti) of the acid in the cup is 22.8°C. Temperature readings are started one minute before addition of second substance. Upon addition of NaOH, the acid temperature increases to a maximum of 28.2°C in one minute and then slowly decreases. The precise determination of Tf is more complicated, since heat exchange is occurring between the contents and the cup during and after the reaction. Evaluation of Tf is accomplished by extrapolation as shown above. This gives a theoretical temperature representing the temperature obtained if instantaneous equilibrium was achieved within the system. By extrapolation, Tf = 29.7°C. The heat capacity for the calorimeter cup is given as 6.80 J/K.
Calculations
NOTE: Since these calculations require only the use of DT, it becomes unnecessary to convert all Celsius temperatures to Kelvin, just to arrive at DT. (Convince yourself this is true!)

To determine the heat of reaction, use Equation 5 and Table 1. (Assume that the heat capacity for a dilute solution of acid in water is very similar to that of water.)


We also need to calculate the heat absorbed by the calorimeter cup.

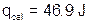
The final heat of reaction value is calculated as follows:
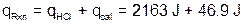

Note that the calorimeter constant is very small compared to the qHCl.
Hess’s Law
If a reaction is carried out in a series of steps, DH for the reaction is equal to the sum of the enthalpy changes for the individual steps.
The overall enthalpy change for the process is independent of the number of steps or the particular nature of the path by which the reaction is carried out. Thus we can use information tabulated for a relatively small number of reactions to calculate DH for a large number of different reactions.
In this experiment we want to know the heat of reaction for burning magnesium metal in oxygen:

This is a very exothermic reaction whose DH of reaction would be extremely difficult to measure using our calorimetry set-up. However, by experimentally measuring the heat of reaction for two other reactions:

and

and using the heat of formation reaction for water:

we can use Hess’s Law to calculate the heat of reaction for magnesium burning in oxygen. Refer to your textbook for further explanation on how to use Hess’s Law. |