         |
 Background Though based on assumptions that gas molecules do not interact with each other and occupy no volume, assumptions you will later learn to be over-simplified, the ideal gas law is still incredibly useful in characterizing the properties of most gases. Mathematically, the ideal gas law is expressed by the equation
The constant R is called the gas constant and takes on a number of different values depending on the units used for pressure. Note that although the units for pressure and volume can vary, the unit for temperature must always be in Kelvins.
In this experiment, you will use the ideal gas law to predict the volume of gas produced from a simple chemical reaction. This reaction will be used to create a mock automobile airbag. Airbags Airbags are safety devices found in most cars being produced today. The reaction used in commercial airbags depends on sodium azide (NaN3), a fairly toxic chemical. When activated, the airbag’s sodium azide rapidly undergoes a decomposition reaction generating sodium metal (Na) and nitrogen gas (N2).
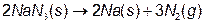
The nitrogen gas inflates the airbag to provide a safety cushion for the passengers in the car. Airbags deploy in 0.015 sec for high-speed crashes and 0.025 sec for low speed crashes. The Reaction Since your laboratory is not equipped to work with chemicals as toxic as sodium azide, we will use sodium bicarbonate (NaHCO3) to produce the gas. When sodium bicarbonate reacts with acetic acid (CH3COOH), carbon dioxide (CO2) and two other products are formed as shown below:
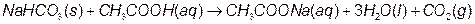
The stoichiometry of this reaction is quite simple since all reactants and products are in a 1:1 molar ratio. Because the overall goal of this experiment is to design an ‘airbag’ that inflates rapidly and fully, without wasting materials, you will need to convert molar amounts of reagents into gram and volume amounts in order to produce the precise volume of CO2 that will fill your ‘airbag’. Stoichiometry and Manipulating the Ideal Gas Law To be able to predict the volume of the gas being produced, you will use the ideal gas law equation. The variables in the ideal gas law are volume, temperature, pressure, and the number of moles of gas. We know that our unknown in the equation is going to be the amount of gas produced. Therefore, we can rearrange the ideal gas law to solve for n:
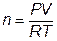
Since we know R is a constant, all we have to measure is the volume of our bag, the atmospheric pressure, and the temperature of our surroundings. For this experiment we will use room temperature and pressure. A thermometer should be used to determine the room temperature and a barometer to measure the atmospheric pressure. With the temperature and pressure taken care of, all that remains is to determine the volume of your ‘airbag’. This can be done by filling the bag with water and then measuring the volume of water. The water also serves the purpose of checking the bag for leaks which would ruin your experimental results. By measuring the volume of gas needed and substituting it, along with room temperature and pressure, into the ideal gas law, you can predict the moles of gas required to fill the ‘airbag’. You can then use simple stoichiometry to calculate the exact amounts of reactants (NaHCO3 and CH3COOH) to produce the correct amount of CO2 needed to fill the bag. 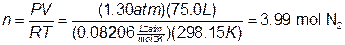Example Problem Substituting these values into our equation as shown, we calculate that we need 3.99-mol of nitrogen gas. Knowing the number of moles of N2 required, we can use the balanced equation given at the beginning of this discussion in order to determine the number of grams of NaN3 needed. Therefore, we need ~173 g of sodium azide to produce 75.0 L of N2.. The calculations just completed are almost identical to those you will perform in this experiment. |
, where P is the gas pressure, V is the volume in liters, n is the number of moles, T is the Kelvin temperature, and R is a constant.
