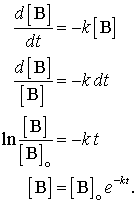
Before going on to the Activation Energy, let's look some more at Integrated Rate Laws. Specifically, the use of first order reactions to calculate Half Lives.

Let's review before going on...

Integrated forms of rate laws:

In order to understand how the concentrations of the species in a chemical reaction change with time it is necessary to integrate the rate law (which is given as the time-derivative of one of the concentrations) to find out how the concentrations change over time.

1. First Order Reactions

Suppose we have a first order reaction of the form, B + . . . . → products. We can write the rate expression as rate = -d[B]/dt and the rate law as rate = k[B]^b . Set the two equal to each other and integrate it as follows:

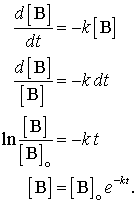
The first order rate law is a very important rate law, radioactive decay and many chemical reactions follow this rate law and some of the language of kinetics comes from this law. The final Equation in the series above iis called an "exponential decay." This form appears in many places in nature. One of its consequences is that it gives rise to a concept called "half-life."

Half-life

The half-life, usually symbolized by t_1/2, is the time required for [B] to drop from its initial value [B]₀ to [B]₀/2. For Example, if the initial concentration of a reactant A is 0.100 mole L^-1, the half-life is the time at which [A] = 0.0500 mole L^-1. In general, using the integrated form of the first order rate law we find that:

Taking the logarithm of both sides gives:

The half-life of a reaction depends on the reaction order.

First order reaction: For a first order reaction the half-life depends only on the rate constant:

Thus, the half-life of a first order reaction remains constant throughout the reaction, even though the concentration of the reactant is decreasing.

Second order reaction: For a second order reaction (of the form: rate=k[A]²) the half-life depends on the inverse of the initial concentration of reactant A:

Since the concentration of A is decreasing throughout the reaction, the half-life increases as the reaction progresses. That is, it takes less time for the concentration to drop from 1M to 0.5M than it does for the drop from 0.5 M to 0.25 M.

Here is a graph of the two versions of the half life that shows how they differ (from http://www.brynmawr.edu/Acads/Chem/Chem104lc/halflife.html)

Let's try a simple problem: A first order reaction has a rate constant of 1.00 s^-1. What is the half life of the reaction?

Since the reaction is first order we need to use the equation: t_1/2 = ln2/k

t_1/2 = ln2/(1.00 s^-1) = 0.6931 s

Now let's try a harder problem:

The half-life of N₂O₅ in the first-order decomposition @ 25°C is 4.03×10⁴s. What is the rate constant? What percentage of N₂O₅ will remain after one day?

There are 24 hours * 60 min/hr * 60 sec/min = 8.64×10⁴ s in a day

So 22.6 % remains after the end of a day.

NOW, Activation Energy:

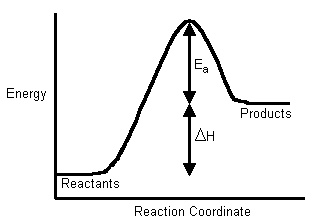
The Activation Energy (E_a) - is the energy level that the reactant molecules must overcome before a reaction can occur.

You probably remember from CHM1045 endothermic and exothermic reactions:

In order to calculate the activation energy we need an equation that relates the rate constant of a reaction with the temperature (energy) of the system. This equation is called the Arrhenius Equation:

Where Z (or A in modern times) is a constant related to the geometry needed, k is the rate constant, R is the gas constant (8.314 J/mol-K), T is the temperature in Kelvin. If we rearrange and take the natural log of this equation, we can then put it into a "straight-line" format:

So now we can use it to calculate the Activation Energy by graphing lnk versus 1/T.

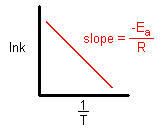
When the lnk (rate constant) is plotted versus the inverse of the temperature (kelvin), the slope is a straight line. The value of the slope (m) is equal to -Ea/R where R is a constant equal to 8.314 J/mol-K.

"Two-Point Form" of the Arrhenius Equation

The activation energy can also be found algebraically by substituting two rate constants (k₁, k₂) and the two corresponding reaction temperatures (T₁, T₂) into the Arrhenius Equation (2).

Let's try a problem:

The rate constant for the reaction H₂(g)  + I₂(g) ---> 2HI(g) is 5.4 x 10^-4 M^-1s^-1 at 326 ^oC.     

At 410 ^oC the rate constant was found to be 2.8 x 10^-2 M^-1s^-1.

Calculate the a) activation energy and b) high temperature limiting rate constant for this reaction.

Answer:

All reactions are activated processes. Rate constant is exponentially dependent on the Temperature

We know the rate constant for the reaction at two different temperatures and thus we can calculate the activation energy from the above relation. First, and always, convert all temperatures to Kelvin, an absolute temperature scale. Then simply solve for E_a in units of R.

Now that we know E_a, the pre-exponential factor, A, (which is the largest rate constant that the reaction can possibly have) can be evaluated from any measure of the absolute rate constant of the reaction.

so

5.4 x 10^-4 M ^-1s^-1 =
A exp{-(1.60 x 10⁵ J/mol)/((8.314 J/K mol)(599K))}

(5.4 x 10^-4 M^-1s^-1) / (1.141x10^-14) = 4.73 x 10¹⁰ M^-1s^-1

The infinite temperature rate constant is 4.73 x 10¹⁰ M^-1s^-1

 

Try one with graphing:

Variation of the rate constant with temperature for the first-order reaction 2N₂O₅(g) -> 2N₂O₄(g) + O₂(g) is given in the following table. Determine graphically the activation energy for the reaction.

T (K)	k (s-1)
298	1.74 x 10-5
308	6.61 x 10-5
318	2.51 x 10-4
328	7.59 x 10-4
338	2.40 x 10-3

 

Answer:

Graph the Data in lnk vs. 1/T. It should result in a linear graph.

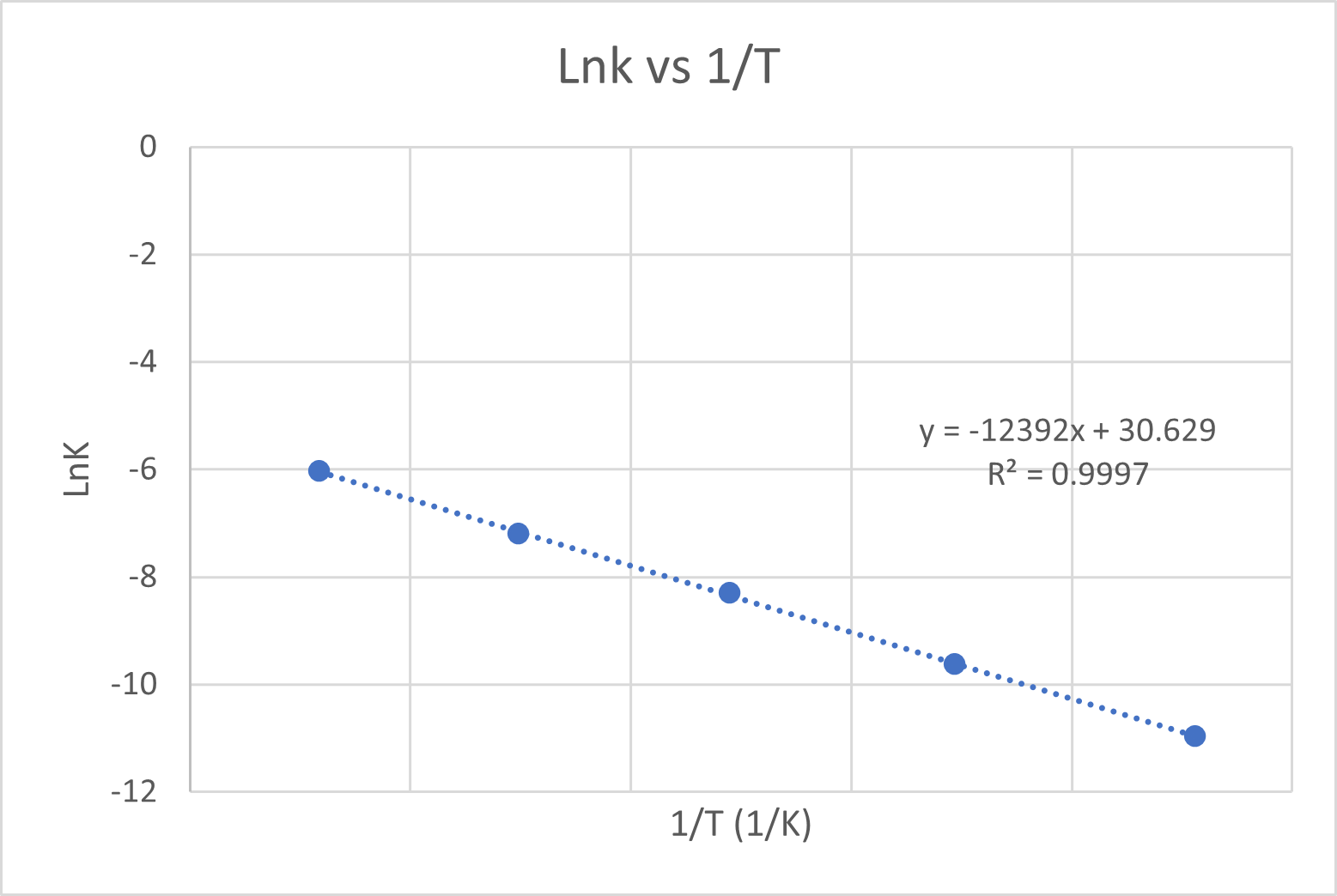
The activation energy can be calculated from slope = -Ea/R. The value of the slope is -8e-05 so:

-12392 = -Ea/8.314 --> Ea = 1.03e5 J/mol or 103 kJ/mol