Buffers

I. Common Ions

A. When a weak acid solution has common ions added by a salt,  the equilibrium will shift by Le Chatelier's principle. The shift in equilibrium position that occurs because of the addition of an ion already involved in the equilibrium reaction is called the common ion effect.

B.  A buffered solution is one that resists a change in its pH when either hydroxide ions or protons are added. Buffered solutions are simply solutions of weak acids or bases containing a common ion. When hydroxide ions are added to a buffer solution they react with the acid and are replaced by the Anions.

C. If you know the ratio of acid to base and both amounts are large the proton concentration can easily be found using the equation:

HH1

To find the pH easily the Henderson-Hasselbalch equation can be used:

 

HH2 


D. Buffer capacity of a buffered solution represents the amount of protons or hydroxide ions the buffer can absorb without a significant change in pH. Most effective buffer solutions contain large amounts of acid and conjugate base.

E. Titrations are commonly used to determine the amount of acid or base in a solution. The progress of an acid-base titration is often monitored by plotting the pH of the solution being analyzed as a function of the amount of titrant added. This is called a pH curve. The optimum area for buffering in a pH curve is in the vicinity where pKa equals the pH (or where the ratio of A- to HA equals 1). The equivalence point is where the amount of protons is equal to the amount of hydroxide ions.

 

F. Indicators are actually weak acids themselves that change color when H+ is added or taken away from the structure. The best indicator for a titration is given by a indicator with pKa or endpoint closest to the pH of the equivalence point.

The Common Buffer Problems

1. Calculate pH given the actual concentrations of the conjugate acid and conjugate base.

 

The pH is easily calculated with:

ex2

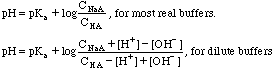
2. The pH shift problem:

If you add 2.00 mL of 0.100 M HCl to 100 mL of a buffer consisting of 0.100 M HA and 0.200 M NaA, what will be the change in pH?

Ka of HA is 1.5x10-5. pKa = 4.82.

The initial pH is: ex3

 

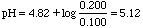
If we add a strong acid to a weak base, such as NaA, they REACT and form new products.

HCl + NaA --> HA + NaCl.

 

(The total ionic equation is H+ + Cl- + Na+ + A- --> HA + Na+ + Cl-)

 

mmoles HCl

mmoles HA
mmoles NaA
Volume, mL
Initial
0.200
10.0
20.0
100+2 mL
Final
0
10.2
19.8
102 mL
Molarities

10.2/102
19.8/102

ex4

3. The "make a buffer of given pH" problem:

We wish to prepare a buffer of pH 10 using common laboratory reagents. How many mL of 6M HCl would we have to add to a solution prepared by adding 100 mL of 15M NH3 to 200 mL of water?

Ka of NH4+ = 5.70x10-10, pKa = 9.24.

HCl + NH3 --> NH4Cl

mmoles HCl

mmoles NH4Cl
mmoles NH3
Volume
Initial
x
0
1500
x/6M + 300mL
Final
0
x
1500-x
x/6M + 300mL
Molarity




We didn't bother computing the molarities, since the volumes cancel out in the buffer equation anyway--a good thing, since the volumes have an "x" in them.

ex5

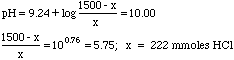
Finally, 222 mmoles HCl/6M = 37.0 mL of 6M HCl needed.

Note that the buffer produced will not actually have a pH of 10. The concentrations are so high that we would need to compute activities from the ionic strengths and generate a corrected value of the Ka for ammonium ion. In an actual lab, we would make up the buffer as calculated above, then use a pH meter and HCl or NH3 to adjust the buffer to 10.0.

 

Now you try some problems:

 

The following is an acid-base equlibrium problem that involves many of the topics we have discussed thus far in chapters 17 and 18. For each of the following solutions:

  1. Describe (in words) what happens.
  2. Write a chemical equation that describes what happens.
  3. What is the proton donor? Why?
  4. What is the proton acceptor? Why
  5. After this solution has reached equlibrium: What species are present? What is their concentration? What is the pH and pOH?
  1. Benzoic Acid (C6H5COOH) is a solid. 15.000 grams is dissolved in distilled water and diluted to 200.00 mL.
  2. Sodium benzoate (NaC6H5COO) is a solid. Used as a preservative in most sodas.  10.000 grams is dissolved in distilled water and diluted to 100.00 mL.
  3. Sodium Hydroxide is a solid. 5.0000 grams is dissolved in 50.0 mL of distilled water.
  4. The benzoic acid solution and the sodium benzoate solution are mixed together in a large flask.
  5. 1.00 mL of the sodium hydroxide solution is added to the buffer.
  6. 10.00 mL of the sodium hydroxide solution is added to the buffer.
  7. 25.00 mL of the sodium hydroxide solution is added to the buffer.

Click Here for the Answers