The direction of spontaneous change is the direction in which total entropy increases. Total entropy change, also called the entropy change of the universe, is the sum of the entropy change of a system and of its surroundings:

DS_univ = DS_sys + DS_surr

According to the second law of thermodynamics, the entropy of the universe, S_univ must always increase for a spontaneous process, that is, DS_univ>0.

Free Energy and Free Energy Change—the Gibbs free energy, G, is used to describe the spontaneity of a process.

G = H - TDS

The free energy change, DG is equal to -TDS_univ and it applies just to a system itself, without regard for the surroundings. It is defined by the Gibbs equation:

DG = DH - TDS

For a spontaneous process at constant temperature and pressure, DG must be negative. In many cases, we can predict the sign of from the signs of DH and DS.

Standard Free Energy Change, DG^o —the standard free energy change, DG^o can be calculated (1) by substituting standard enthalpies and entropies of reaction and a Kelvin temperature into the Gibbs equation or (2) by combining standard free energies of formation through the expression

Summary of Gibbs free energy

Problems:

1) In the Haber process for the manufacture of ammonia

At what temperature will the reaction above become spontaneous?

The fact that both terms are negative means that the Gibbs free energy equation is balanced and temperature dependent:

ΔG = ΔH - TΔS

below this temperature the reaction is spontaneous.

2) Determine the Delta G under standard conditions using Gibbs Free Energies of Formation found in a suitable Thermodynamics table for the following reaction:

4HCN(l) + 5O₂(g) ---> 2H₂O(g) + 4CO₂(g) + 2N₂(g)

1. Check to make sure the equation is balanced
2. Look up the Standard Free Energy of Formation of H₂O(g) and multiply by its coefficient(2) in the equation.

2 moles ( -237.2 kj/mole) = -474.4 kj = Standard Free Energy of Formation for two moles H₂O(l)

3. Look for the Standard Free Energy of Formation of CO₂(g) and multiply by its coefficient (4)

4 moles ( -394.4 kj/mole) = -1577.6 kJ = Standard Free Energy of Formation for four moles CO₂

4. Look up the Standard Free Energy of Formation of N₂(g) and multiply by its coefficient(2)

2 moles(0.00 kj/mole) = 0.00 kJ = Standard Free Energy of Formation for 2 moles of N₂(g)

5. Add the results of steps 2,3, and 4 to get the Standard Free Energy for the products

(-474.4 kJ) + (-1577.6 kJ) + 0.00 = -2052 kJ = Standard Free Energy for Products

6. Look up the Standard Free Energy of Formation for HCN(l) and multiply by its coefficient(4)

4 moles ( 121 kj/mole) = 484 kJ = Standard Free Energy for 4 moles HCN(l)

7. Look up the Standard Free Energy of Formation of O₂(g) and multiply by its coefficient(5)

5 moles (0.00 kJ/mole) = 0.00 kJ = Standard Free Energy of 5 moles of O₂(g)

8. Add the results of steps 7 and 8 to get the Standard Free Energy of the Reactants

(484) + (0.00) = 484 kJ = Standard Free Energy for Reactants

9. Subtract the result of step 9 from the result of step 5 to get the Standrad Free Energy Change for the Reaction

Sum of Free Energy of Products - Sum of Free Energy of Reactants = (-2052 kJ) - (484 kJ) = -1568 kJ = Standard Free Energy Change for the Reaction.

3) For the following reaction using the Thermodynamics table:

CoCl₂(g) ---> CO(g) + Cl₂(g)

1. Calculate at 127°C the DG
2. Calculate the Temperature when the above reaction is at equilibrium (DG = 0)
3. At what temperature will this reaction be spontaneous?

1. Check to see if the equation is balanced
2. Determine the Delta H of the Reaction using Hess Summation Law and Standard Enthalpies of Formation

Delta H = Sum of Delta H_f of products - Sum Delta H_f of Reactants

Delta H = [ 1(-110.5) + 1(0.00)] - [ 1(-220)]

Delta H = -110.5 - (-220) = +110.5 kJ

3. Determine Delta S for the reaction using Standard Molar Entropies and Hess Law of Summation

Delta S = Sum Standard Molar Entropies of Products - Sum of Standard Molar Entropies of Reactants

Delta S = [ 1 mole(197.5 J/mole-K) + 1 mole(223) J/mole-K] - [ 1 mole(283.7 J/mole-K)]

Delta S = 420.5 J/K - 283.7 J/K = 136.8 J/K

4. Convert Delta S from J/K to kJ/K

136.8 J/K X 1 kJ / 1000 J = 136.8 / 1000 = .1368 kJ/K

5. Convert 127 C to K

K = C + 273 = 127 + 273 = 400 K

6. Plug results of step 2 and 4 into Gibbs Helmholtz Equation along with Kelvin Temperature to get Delta G of the Reaction

Delta G = Delta H - T(Delta S)

Delta G = 110.5 kJ - 400 K(.1368 kj/K)

Delta G = 110.5 - 54.72 kJ = + 55.78 kJ

Because this reaction has a positive Delta G it will be non-spontaneous as written.

Name of Species         Delta Hf(kJ/mole)      Delta Gf(kJ/mole)      S(J/mole-K)

CO₂(g)                          -393.5                           -394.4                            213.7

CH₃OH(l)                     -238.6                           -166.2                            127

COCl₂(g)                      -220                              -206                               283.7

CO(g)                            -110.5                           -137.2                            197.5

C₂H₂(g)                         227                                209                                200.9

Cl₂(g)                            0                                    0                                    223

HCN(l)                          105                               121                                112.8

H₂O(g)                          -241.8                           -228.6                           188.7

H₂O(l)                           -285.8                           -237.2                           69.9

HNO₃(aq)                     -206.6                           -110.5                           146

N₂(g)                             0                                     0                                   191.5

NO₂(g)                          33.2                              51                                  239.9

NO(g)                           90.3                              86.6                               210.7

O₂(g)                             0                                    0                                    205

CS₂                                                                                                            151

H₂                                  0                                    0                                    130.6

CH₄                               -74.8                             -50.8                             186.3

H₂S                                -20.17                           -33.01                           205.6

SO₂                                                                                         248.1

Free Energy and Equilibrium.

Because DG is a measure of how favorable a reaction is, it also relates to the equilibrium constant.

1. A reaction with a negative DG, is very favorable, so it has a large K.
2. A reaction with a positive DG is not favorable, so it has a small K.
3. A reaction with DG = 0 is at equilibrium.
4. There are several different DG's.  It is important to distinguish between them.
1. DG^o (a delta G, with a superscript o), is the free energy change for a reaction, with everything in the standard states (gases at 1 bar, and solutions at 1 M concentration), and at a specific temperature (usually 25°C)
2. DG (just delta G). This is the free energy change for a reaction that is not at the standard state.
5. The DG's are related as follows. KNOW THIS EQUATION and understand how to use it:

DG =DG^o + RT ln Q

Where Q is the same Q we used for calculating equilibrium (K is the special case for Q when at equilibrium.)

2. Spontaneity and Speed of Reactions. This section simply points out that there is not any direct relationship between DG and the speed of a reaction (kinetics).

Problem:

Starting with the change in free energy at constant temperature: DG° = DH° - TDS°, and with the relation between DG and equilibrium constant, K: DG° = -RT lnK, derive a linear equation that expresses lnK as a function of 1/T (a linear equation is of the form y = mx + b).

(b) The equilbrium constants for the conversion of 3-phosphoglycerate to 2-phosphoglycerate at pH 7 is provided:

Calculate DG° at 25°C.

(c) What is the concentration of each isomer of phosphoglycerate if 0.150 M phosphoglycerate reaches equilbrium at 25°C.

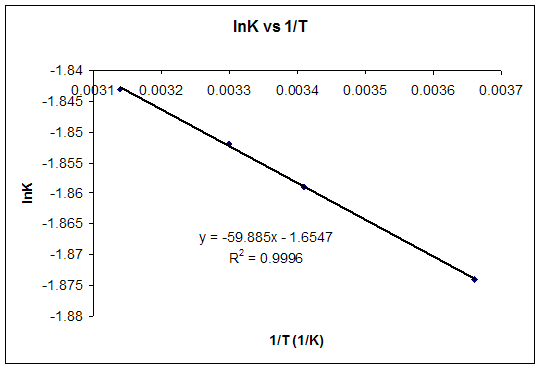
b) For T = 25ºC, using the equation of the graph, lnK = -1.8557 and K = 0.1564.

c)