Fun Stuff: Solving a Rubik's Cube
What is more satisfying than solving a Rubik's cube? Making a computer solve one for you.
Background
In graduate school, one of my lab mates and I had a competition see who could first develop a working code to solve a Rubik's cube. I think I won, but seeing as the other party is not here to defend himself, yes, I definitely won.
In this tutorial, I will outline the basic development process I used and provide you with enough of the infrastructure code so that you can implement your own algorithm.
The C++ code for my Rubik's cube solver can be found here.
Now, the basic design process:
Step 1. Develop a framework that allows you to represent the cube. In cube.cpp and cube.hpp, you will find the RubiksCube class with member varibles and functions available to represent the data in the cube and to manipulate the cube. Aside from an internal representation of the data, you will want to have some way of actually visualizing the cube. For this tutorial, I have done that work for you; the cube is displayed using OpenGL.
Step 2. Develop functions to perform basic operations to manipulate the cube. These include all of the standard operations you might find in any online Rubik's cube tutorials (right face: clockwise rotation, etc.). I have also taken the liberty of coding each of these operations so that you can focus on the actual algorithm for solving the cube.
Step 3. Develop algorithms that can recognize the current state of the cube and apply appropriate operations to work toward the solution. In principle, you can apply any algorithm you want. Just google "how to solve a Rubik's cube" for some examples.
Interactive Rubik's Cube
Before diving into the details of the code, if you're here because of an affinity for cubing and are terrified of C++, fear not. You can compile this code in an interactive mode that will let you solve the cube using keyboard inputs. You simply need to use the following flags in the Makefile before compiling:
CFLAGS = -O2 -DVISUAL -DINTERACTIVE #-DLINUXIf you're using a Mac with OpenGL installed, this should be sufficient. If you're using a linux machine, then you will need to uncomment the linux flag.
Once you have compiled the code, execute it, and you should be able to use the following commands
r = rotate right face clockwise R = rotate right face counterclockwise l = rotate left face clockwise L = rotate left face counterclockwise f = rotate front face clockwise F = rotate front face counterclockwise b = rotate back face clockwise B = rotate back face counterclockwise u = rotate top face clockwise U = rotate top face counterclockwise d = rotate bottom face clockwise d = rotate bottom face counterclockwise left, right, up, down arrows = rotate the cube
The RubiksCube class
In cube.cpp and cube.hpp, you will find enough functionality for you to design your own algorithm to solve the Rubik's cube. Recall that the visualization of the cube is handled by OpenGL, and the main function containing the logic to solve the cube is the "display" function used by OpenGL in main.cpp. You can create a new pointer to a RubiksCube object there:
void display(void){
// clear
glClear (GL_COLOR_BUFFER_BIT);
glTranslatef(-.05,0.05,0);
// pointer to cube object
std::shared_ptr<RubiksCube> cube (new RubiksCube());
// your solution goes here!
}
The RubiksCube class has a number of public functions that allow you to
perform basic operations to manipulate the cube:
class RubiksCube
{
public:
/// constructor
RubiksCube();
/// denstructor
~RubiksCube();
/// bring face to front
void BringToFront(int face);
/// bring face to top
void BringToTop(int face);
/// rotate right face clockwise
void MoveR();
/// rotate right face twice
void MoveR2();
/// rotate right face counterclockwise
void MoveRprime();
/// rotate left face clockwise
void MoveL();
/// rotate left face twice
void MoveL2();
/// rotate left face counterclockwise
void MoveLprime();
/// rotate upper face clockwise
void MoveU();
/// rotate upper face twice
void MoveU2();
/// rotate upper face counterclockwise
void MoveUprime();
/// rotate lower face clockwise
void MoveD();
/// rotate lower face twice
void MoveD2();
/// rotate lower face counterclockwise
void MoveDprime();
/// rotate front face clockwise
void MoveF();
/// rotate front face twice
void MoveF2();
/// rotate front face counterclockwise
void MoveFprime();
/// rotate back face clockwise
void MoveB();
/// rotate back face twice
void MoveB2();
/// rotate back face counterclockwise
void MoveBprime();
/// print cube in 2D format
void PrintCube();
/// print cube in 3D
void PrintCube3D();
/// return total number of moves
int total_moves(){ return moves; }
protected:
/// cube data
int **cube_data;
...
Note that the actual state of the cube is stored in int **cube_data, which
is a protected member of the class. So, if you want to access cube_data
directly, then you either need to extend the RubiksCube class to include
your algorithm functions or develop a derived class that includes these
solver functions. I have taken the latter approach, and you can find
the RubiksCubeSolver class in the link to my code above
(see cube_solver.hpp and cube_solver.cpp). Either way,
cube_data[face][square] will contain an integer that corresponds to the
color of a given square located on a given face. The indexing schem I use
is
b 3
l u r 2 0 4
f d 1 5
0|1|2
3|4|5
6|7|8
0|1|2 0|1|2 0|1|2
3|4|5 3|4|5 3|4|5
6|7|8 6|7|8 6|7|8
0|1|2 0|1|2
3|4|5 3|4|5
6|7|8 6|7|8
As an example, here is my solution, as executed with the RubiksCubeSolverClass:
void display(void){
// clear
glClear (GL_COLOR_BUFFER_BIT);
glTranslatef(-.05,0.05,0);
// your solution goes here!
std::shared_ptr<RubiksCubeSolver> cube (new RubiksCubeSolver());
cube->LocateOrigin();
cube->FormCross();
cube->SolveTopLayer();
cube->SolveMiddleLayer();
cube->FormBottomCross();
cube->PermuteBottomCorners();
cube->OrientBottomCorners();
cube->PermuteBottomEdges();
printf("\n moves to solution: %3i\n",cube->total_moves());
}
Obviously I've hidden all of the complexity of actually assessing the state
of the cube at any given step, but the overall algorithm just looks
like any other one you might find online.
Here you can see the step-by-step progression my
code takes, along with the visualization of the cube.
cube->LocateOrigin();
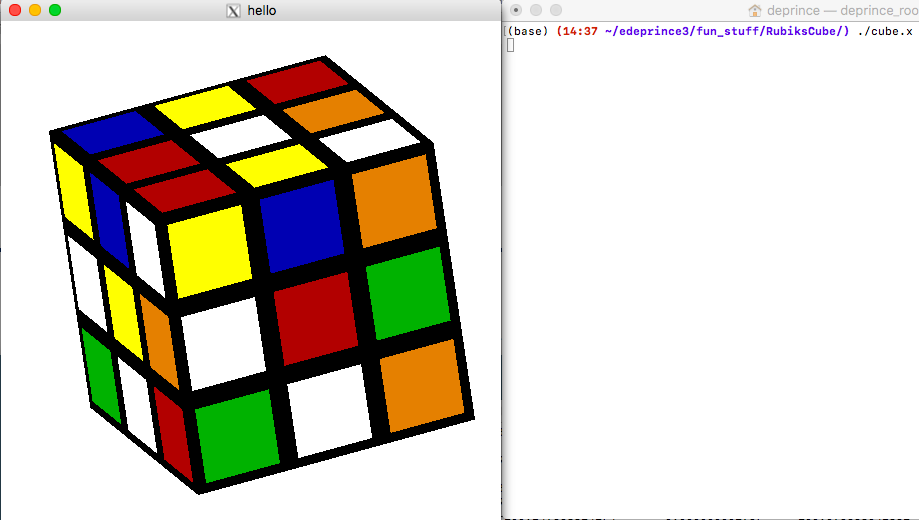
cube->FormCross();
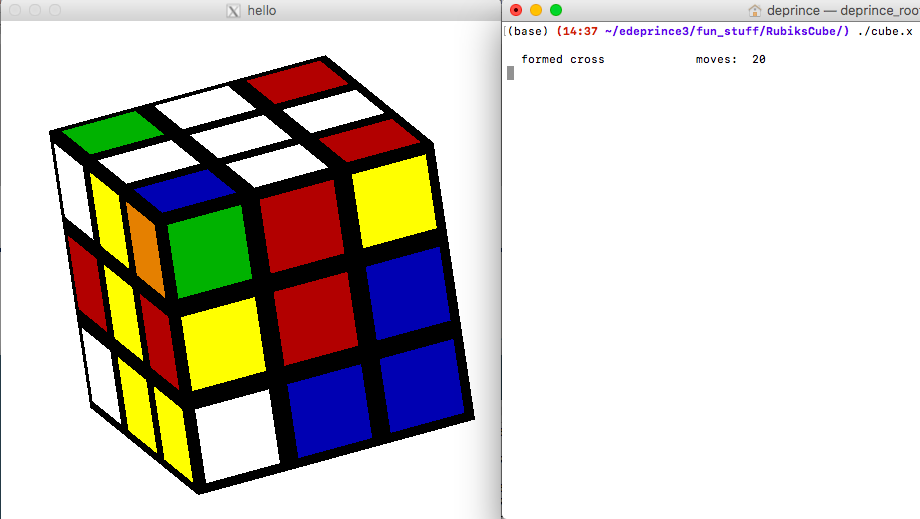
cube->SolveTopLayer();
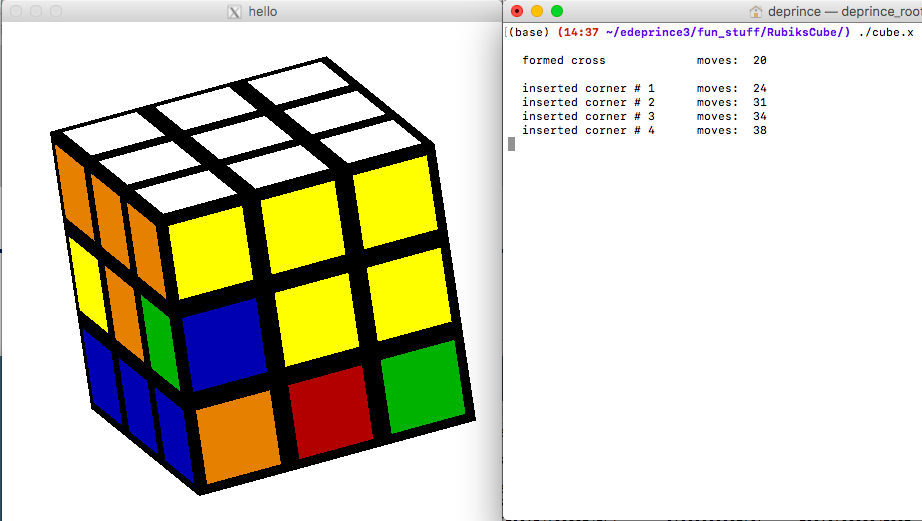
cube->SolveMiddleLayer();
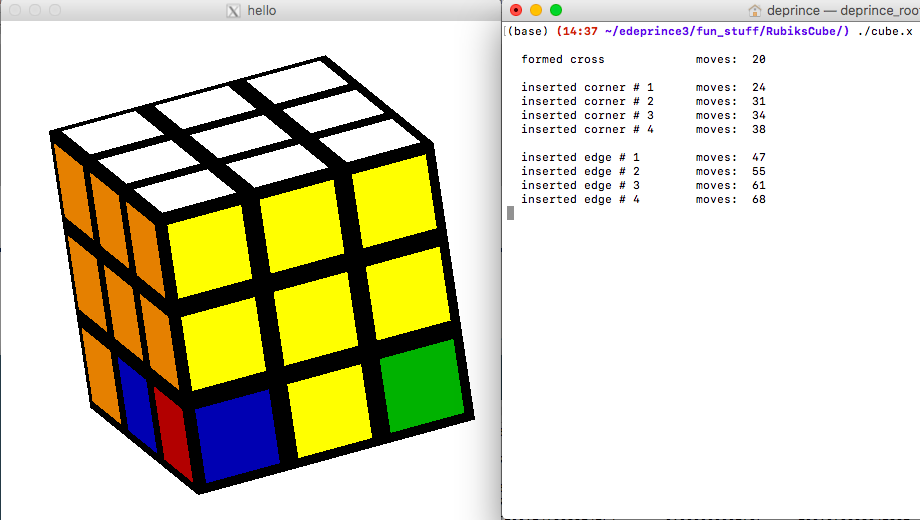
cube->FormBottomCross();
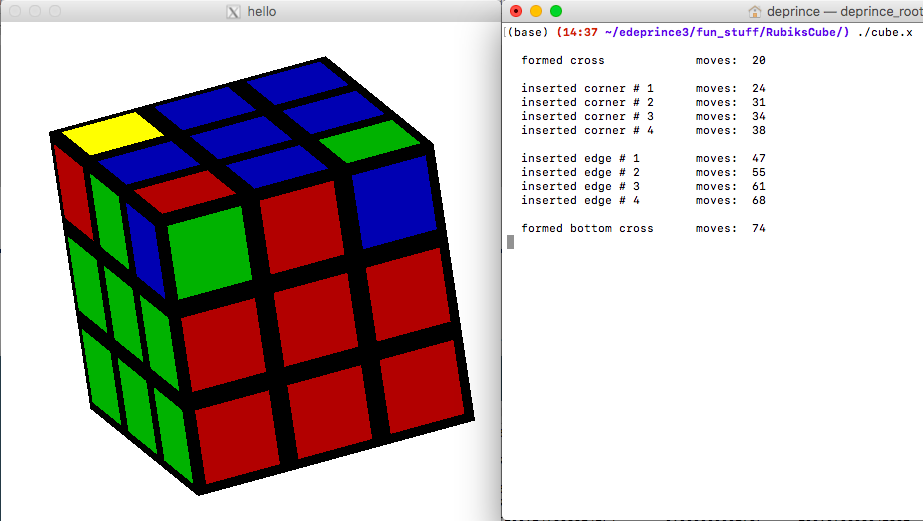
cube->PermuteBottomCorners();
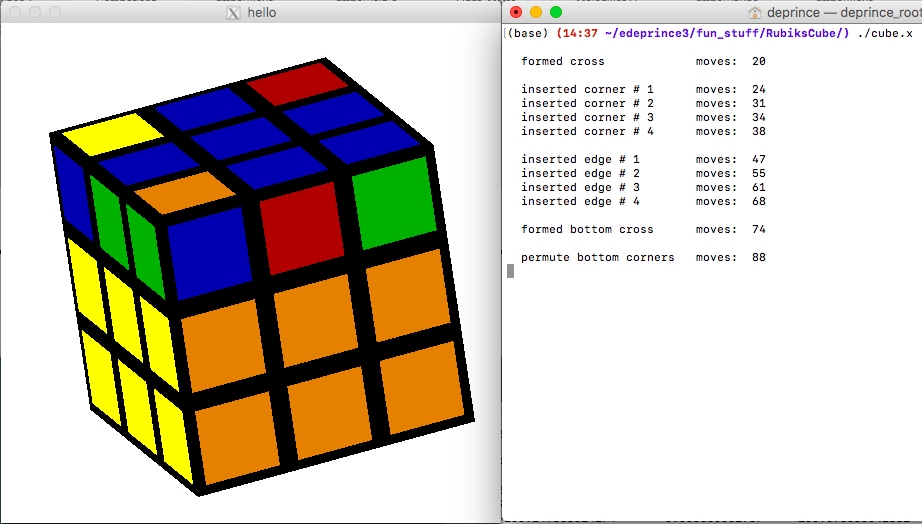
cube->OrientBottomCorners();
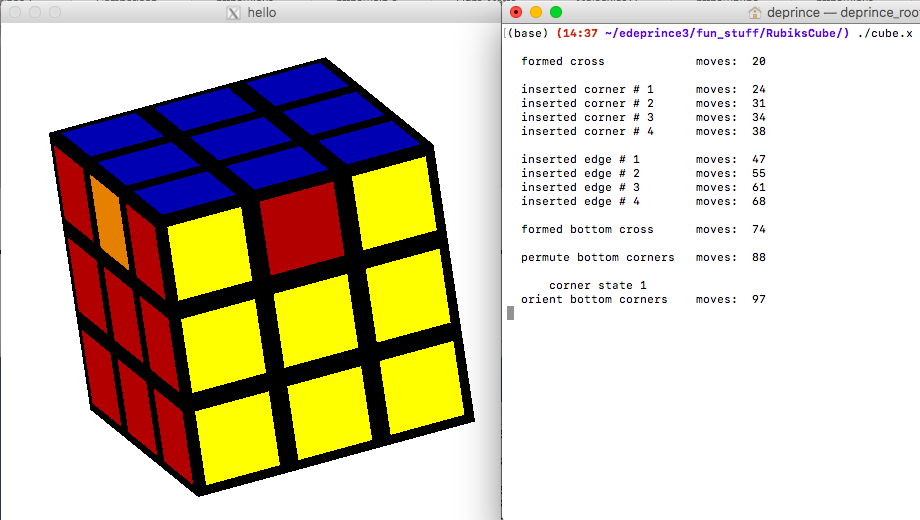
cube->PermuteBottomEdges();
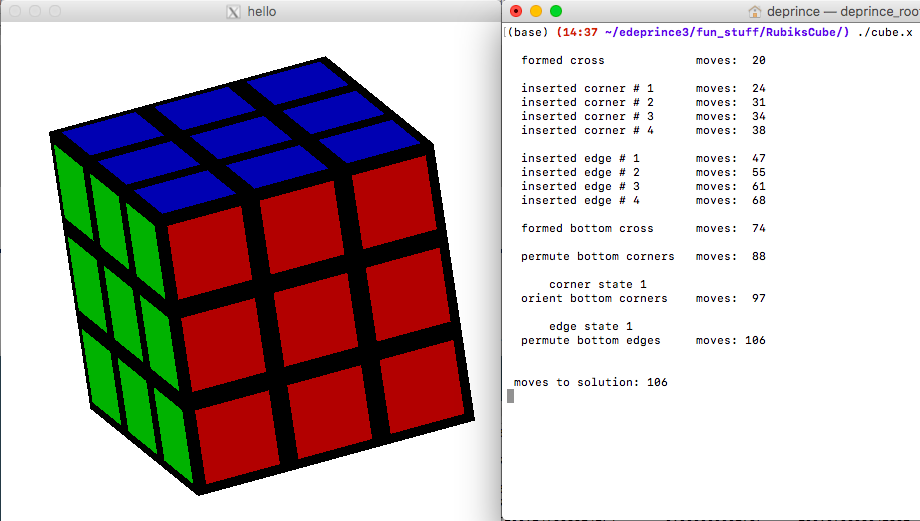
Your Rubik's cube solver
Your challenge is to develop a solver that can assess the state of the cube and apply appropriate algorithms to work toward the solution. The majority of the complexity will be in assessing the state of the cube. Once you understand the state of the cube, manipulating it is straghtforward. For example, in the last step above (permute bottom edges), the cube is identified to be in "edge state 1" (what that state is, precisely, is irrelevent for the moment). Given that state, a specific algorithm can bring the cube to full solution:
void RubiksCubeSolver::EdgeState1Algorithm(){
MoveR2();
MoveU();
MoveF();
MoveBprime();
MoveR2();
MoveFprime();
MoveB();
MoveU();
MoveR2();
}






