CHM 1020 Fall 2000 Chapter 1 Lecture Notes

The course organization, syllabus, and tentative lecture schedule were discussed. Some communication in the course will be by electronic mail, and students must have a garnet email account in order to receive this mail. The university has a web site that explains everything you need to know about getting a computer, setting it up, and getting your email account activated. Some materials and supplementary information will be available on a web site supporting the course. One portal to this web material is through Blackboard's CourseInfo, though there is another that bypasses CourseInfo if that server has problems.

The text book (Hill and Kolb, Chemistry for Changing Times, 9^th Ed. Prentice Hall, NJ, 2001) comes shrink wrapped with a study guide, which will provide extra supplementary problems for students to practice on, a CD ROM computer disk with practice on some skills like balancing equations, and an internet guide to chemistry on the internet. These latter items did not cost extra and can provide a means of further study and exploration if the student wishes to use them.

Chemistry is study of matter and changes it undergoes. Let's take a look at a few examples of what we mean.

Chemistry is a science. Science involves continual interaction between experimental observation and model development. The demonstrations we just went through are examples of observations. We have to learn how to make them consistently and describe them clearly. Often will involve making careful measurements. But then we want to know what causes the things we see. Why are some things solids, others gases, i.e. why do melting and boiling points differ? Why are some things combustible, others not? What is happening in a chemical change?

Models are developed to explain observations, then the models suggest more experiments to test the models.

Repeatable observations are known as facts. Models developed to explain facts at first are hypotheses, but when supported by sufficient experimental information can become theories.

The early Greeks were philosophers who loved to theorize, but lacked the experimentation necessary to test the theories. They argued whether matter was continuous or consisted of discrete particles (atoms) but had no data to support either idea. They also speculated on the nature of matter from its properties. Combining the opposites hot and cold, with the opposites wet and dry, they suggested everything was composed of some combination of four basic elements, earth, air, fire, and water, depending on the combination of these properties as shown in the following diagram.

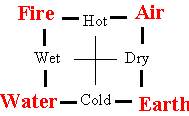
The Greeks, though, did not use their theoretical musings to suggest experimental tests that could verify or disprove these ideas.

In the middle ages, alchemists discovered many chemical reactions and developed many experimental observations on chemical change in their hunt for a method to change a base metal (lead) into gold. They did not develop theoretical models to organize and explain these observations, however, so they did not progress with a proper understanding of nature either.

Experiments by chemists like Robert Boyle, Lavoisier, and others finally began to make a connection between theory and experiment, and thus the methods of modern science were born.

Just as one example of how models are developed, tested, then revised, we can use an early theory of the chemical change of combustion. It was recognized that combustion and rusting (calcinations) of metals were similar reactions. It appears that the flame of a combustion process represents something being lost to the surroundings, so the theory was developed that combustion represents the loss of a substance that was given the name phlogiston. When a candle in a closed container would no longer burn, it was thought the air had absorbed all the phlogiston it could hold. The gas produced by the decomposition of mercury "calx" would support combustion very brightly. The interpretation was that the mercury calx combined with phlogiston to form mercury and "dephlogisticated air" or "fire air". Scheele and Priestly independently discovered this gas.

But a metal calx was known to be heavier than the metal. For this theory to be correct, phlogiston must have a negative mass. Finally careful measurements of the mass all components of the reaction by Lavoisier concluded that what was actually going on was the conversion of calx of mercury into mercury and a gas known as "vital air". Lavoisier finally called this vital air "oxygene". The phlogiston theory was overturned in favor of the theory that combustion was a reaction of a substance with oxygen, and a metal "calx" was a metal oxide.

So from this example, we can see that not only careful experimentation and observation are necessary, but measurement is a part of this observation.

Chemistry is defined as the study of matter and the changes it undergoes. Matter is defined as anything that occupies space and has mass. Lets look in a bit more detail at matter.

We generally observe matter in one of three states. Following are the observable properties of these state, as well as our theoretical model developed to explain these properties. See also Figure 1.8 in the book for a pictorial representation. Matter can change states by raising or lowering the temperature. Some matter we only observe in a single state unless we go to extremes of temperature. (Recall liquid nitrogen from our first day demonstration).

Matter can be subdivided into two classes: mixtures and pure substances. The distinction at first is an operational one (i.e. based on experimental operations. A substance is defined as pure when all efforts to purify it cause no further change in its properties.

Elements

There are 109 known elements. Only about 90 occur naturally. The rest have been made artificially. You should learn the names and symbols for the common elements shown in Table 1.3. These will be part of your “vocabulary” you need to speak the language of chemistry.

Among those not on this list, some are named for places (Californium, Berkelium) and some for people (Einsteinium, Lawrencium, Rutherfordium).

The person discovering a new element usually is given the privilege of naming it. In the case of recent disputes over who was first to discover elements, there has been controversy over naming, and just recently has an international committee settled on the names of the most recently discovered elements.

The elements are organized very neatly by chemical properties in an arrangement known as the periodic chart. One example is shown on the inside cover of your textbook. There are now many web sites that publish versions of the periodic chart, including detailed information about the chemical and physical properties of each of the elements.

How do we understand and interpret this organization in the periodic chart? That is one of the major questions we will try to clarify in the next few chapters of this course. The organization is based both on measurable properties as well as on our theoretical models used to describe elements. To begin the discussion of these models and their relationship to properties, we must begin with a discussion of measurement in science.

Scientists world-wide use a system of measurement known as the Système Internationale (SI). This is a slight variation of what used to be known as the metric system. The basic units of the system are summarized in Appendix A of your text.

Temperature is a property of matter that changes as heat energy is added or taken away. Heat is a form of energy that flows spontaneously from a hot body to a cold body. These statements, which represent our every day experience, represent observations. Our theoretical interpretation of temperature and heat depend upon our model for describing the nature of matter. We will see that our model for matter suggests it is composed of tiny particles in motion (see the description of gases, liquids, and solids above), and in this model the heat added to an object increases the energy of motion of the particles (the kinetic energy) and temperature is just a measure of the average kinetic energy of the particles.

We measure temperature on the basis of a property of a substance that depends on it. In a thermometer, that property is the volume of a liquid such as mercury. In a thermocouple, it will be the electrical conductivity between two different metals.

These devices are calibrated with reference to some defined temperature. In particular, the temperature at which water changes first from a solid to a liquid (the melting point), then the temperature at which it changes from a liquid to a gas (the boiling point). Since these temperatures vary with atmospheric pressure (water boils at a lower temperature in the mountains where the pressure is lower, or at a higher temperature in a pressure cooker), we specify a pressure of 1 atmosphere as a condition.

Our everyday temperature scale in the US is the Fahrenheit scale. It sets the freezing point at 32^oF and the boiling point at 212^oF, with a division of 180 degrees between these points on the scale. Scientists use the Celsius scale, where the freezing point is 0^oC and the boiling point is 100^oC, with a division of 100 degrees between these points. Therefore one Celsius degree is 180/100 or 9/5 of a Fahrenheit degree.

The formula for conversion between Fahrenheit and Celsius is only slightly complicated algebraically, but you will not be required to calculate exact conversions:

Studies with gases, and theoretical considerations we don’t want to get into yet, establish that there is a temperature that we cannot go below—a temperature in which there is the minimum possible kinetic energy in the particles of matter. This temperature is called absolute zero, and has a value of –273.16 ^oC. Scientists often use this value as zero on another scale, known as the Kelvin scale. The conversion between ^oC and K is very simple, and you will be expected to be able to do this calculation:

Heat energy flows between bodies that are at different temperatures. If two bodies at a different temperature are brought together, heat will flow from one to another until the temperatures become equal.

Heat energy is therefore measured in terms of the temperature change it can cause in a substance. The early unit of heat energy was the calorie, which was defined as the amount of heat required to raise the temperature of one gram of water by 1 ^oC or by 1 K (since the size of these degrees are the same). We can then use this definition to measure quantities of heat produced, for example, in a chemical reaction, by employing a calorimeter which is simply a large container of water in which the reaction vessel is placed. When heat is produced, it causes the temperature of water to increase, and knowing the amount of water and the temperature increase allows one to calculate the quantity of heat.

Our model for the structure of matter explains heat energy as constituting the mechanical energy of the particles making up matter, i.e. energy of motion of the particles (kinetic energy) and energy of attraction between the particles (potential energy). In this model temperature is related to the average kinetic energy of the particles. The more heat that is added, the higher the kinetic energy, and therefore the higher the temperature.

Heat is only one form of energy, and we will consider other forms later. Different units of measurement are sometimes used in the other forms, depending on convenience and the way the measurements are made. All energy units are related, though, and the SI system of nomenclature has adopted the joule as the basic unit of energy, and relates other units to the joule. The calorie has been re-defined as exactly 4.184 joules.

Incidentally, the Calorie, with a capital C, is a unit often associated with nutrition. It is actually equal to 1000 calories, or a kilocalorie.

That last observation points up an important feature of the SI system, in that one can more conveniently change the size of units. Rather than comparing inches to feet to miles when one wants to compare short and long distances, the size of a unit is changed by adding a prefix to it. The prefix indicates multiplication of the unit by a power of ten. Table 1.2 of your text summarizes these prefixes. For this class, I expect you to remember only the following prefixes:

Unit

Abbreviation

Numerical
Equivalent

mega

10⁶

kilo

10³

deci

10^-1

centi

10^-2

milli

10^-3

micro

10^-6

All measurements are limited by our ability to make them accurately and precisely. Accuracy refers to how close our measurement is to the true value of the quantity. Precision refers to how well we can reproduce the measurement making it repeatedly.

Units are part of calculations. How many breaths have you taken in your lifetime? (Make an assumption--30 breaths/minute). Then do the unit conversion:

But not justified in writing this many figures even if that is what the calculator gives. Both the 20 yrs and 30 breaths have uncertainty in the second digit, so are good to only two significant figures. Therefore the answer should be written to two significant figures, and as a large number is better written in exponential notation:

(Note: at about 3 x 10²² particles of air/breath, this is 9 x 10³⁰ particles of air breathed over the 20 year period).

0.0023 (only two. Can be written 2.3 x 10^-3. The zeros only mark the decimal position).

6.1000 (five. The zeros aren't necessary to mark the decimal position-their only function is to say that the number is know to be between 6.0999 and 6.1001).

In multiplication or division, the answer should have the same number of significant figures as the least significant number in the calculation. In addition and subtraction, the least significant decimal position is determined from the least significant decimal position in the numbers being added or subtracted. For example 2.15 + 0.1239888, the answer would be significant only to the hundredths position. (Image adding 2.15?????? to 0.123988, you see there is uncertainty in the thousandths position).

Refer to Appendix A for further elaboration, and to this web site for some practice in determining significant figures in numbers.

Note in this example, we also had to deal with a very large number. In scientific measurements, we often deal with very large and very small numbers, therefore we use exponential notation to express them.

Another way of dealing with larger or smaller numbers is the use of prefixes to our units of measurements. Refer to Table 1.2 for the common prefixes in the metric system.

Measurements therefore are numbers with units. They are meaningless without the units. And the units are involved in any calculation involving numbers. Keeping units straight makes it simpler to convert one quantity to another.

Some measurements are a combination of quantities. Density is an example. Recall the demo of the ice floating on one liquid (water) and sinking in another (alcohol) because the density was different. Density of liquids and solids is often given in g/mL, while density of gases may be given in g/L.

Chemistry 1020--Lecture Notes--Chapter 1

State

Properties

Model

Element

Compound

Elements

Unit


CHM 1020--Chemistry for Liberal Studies--Fall 2000