CHM 1020--Chemistry for Liberal Studies--Fall 2000

Chapter 2 Notes

Quantitative Laws of Chemical Reactions

 A summary of factual information that is repeatable is sometimes stated in the form of a scientific law.  We discussed earlier that Lavoisier made careful measurements of the masses of reactants and products in a chemical reaction.  From his findings, and the findings of others, we can state the law of conservation of mass:  the mass of reactants in a chemical reaction is equal to the mass of products.  In other words, in a chemical reaction matter is neither created nor destroyed.

 A second set of observations about the composition of compounds from the work of Joseph Proust and others is summarized in our definition of a compound (a substance composed of two or more elements in definite proportion by mass).  This became the law of constant composition (or the law of definite proportions):  A given compound always contains elements in a definite proportion by weight.  Experiments by Berzelius illustrate this law.  One can mix lead and sulfur and heat to form lead sulfide.  These elements always react in a definite ratio:  1.56 g of sulfur for every 10.00 g of lead.  If one adds more sulfur than this, sulfur is left over.  If one has less sulfur than this, lead is left over.  (See Figure 2.5 to illustrate).

An English schoolteacher, John Dalton, saw in these laws the experimental validation of the idea that matter is composed of discrete particles, or atoms.  In fact, he added one more law of his own.  He noted that sometimes to elements reacted in different proportions to form different compounds.  For example, carbon and oxygen react in a proportion of 3 g carbon to 4 g oxygen to form the compound carbon monoxide.  But they also react in the proportion of 3 g carbon to 8 g oxygen to form carbon dioxide.  The amounts of oxygen reacting with a fixed weight of carbon (4 and 8 g reacting with 3 g) were in a small whole number ratio to each other (4:8 = 1:2).  Dalton stated this as the law of multiple proportions.

Another example of this law is shown by three oxides of nitrogen:  nitrous oxide, nitric oxide, and nitrogen dioxide.  The relative masses of nitrogen reacting with 1.0 g of oxygen are 4:2:1 (see Table 2.1).

These quantitative laws were the basis for Dalton’s statement of his Atomic Theory, a model he used to explain the observations.  Following are the basic tenets of his theory:

1. All matter is composed of tiny particles called atoms.
2. All atoms of a given element are alike, but atoms of different elements are different.  (In particular, he was referring to the mass of the atoms).
3. Compounds consist of particles containing two or more atoms combined in a fixed number ration.  (We now call these particles molecules).
4. Chemical reactions simply involve rearrangements of atoms.  No atoms are created, no atoms are destroyed.

Lets see how these tenets explain the observations:

 Law of conservation of mass.  The number of atoms don’t change, therefore the total mass doesn’t change.

Law of definite composition… Each particle (molecule) of a compound has a definite proportion of atoms, therefore a definite mass composition of the atoms.  Therefore a large number of the molecules will all have this same composition.  Note Figure 2.7 which illustrates that explains Berzelius’ experiments with lead and sulfur.  Lead and sulfur atoms combine in a 1:1 ratio.  If there are too many sulfur atoms, sulfur is left over.  If there are too many lead atoms, lead is left over.

Law of multiple proportion.  Carbon dioxide contains two atoms of oxygen per atom of carbon, while carbon monoxide contains only one.  The amount of oxygen reacting one atom of carbon must be in a whole number ratio.  Even with the more complicated nitrogen oxides, we see the following relationships: 

 From these relationships, it was possible to calculate the ratio of masses of atoms, without knowing the actual mass of any given atom.  To do that, though, required some insight into the relative numbers of atoms in a molecule.  Dalton thought that water would have the simplest possible composition:  one atom of hydrogen for one atom of oxygen, or HO.  The relative weights of hydrogen and oxygen in water are 1:8 (11%/89% or 11g/89g).  Therefore Dalton thought that an oxygen atom would have 8 times the mass of a hydrogen atom.

We now know, of course, that water is H₂O.  (Note the way we symbolize atomic composition, using subscripts to refer to the number of atoms, and the elemental symbol to stand for the atom).  Therefore the relative masses of an oxygen atom to a hydrogen atom must be 16:1. 

If the mass of carbon and oxygen in carbon monoxide is 3:4, and there is one atom of each in this molecule, then the mass of carbon must be 12 on this scale.  Confirmation of this relative mass could be obtained from the composition of methane, CH₄, which contains 75% C and 25% H, a mass ratio of C/4H of 3:1, or of C/H of 12:1. 

As the composition of more compounds became available, and the accuracy of measurements improved, the reference for the scale was changed from hydrogen to oxygen, assigning a value of 16.000 to oxygen.  As we learned more about atomic structure, and developed techniques like mass spectrometry which was able to show that atoms of a particular element were not all alike in mass, but consisted of isotopes of different masses (some oxygen atoms with a mass of 16, some with a mass of 17, some with a mass of 18), the scale was then re-defined with t he standard being the isotope of carbon having a mass of 12 exactly. 

Our current atomic weight scale show averages for the isotope masses.   

Scientists began to try to organize information about the known elements, and the atomic weight was an obvious property to use for the organization.  Listing elements in the order of increasing atomic weight created a periodic repeat in chemical properties.  One of the first to do this, and to also recognize there needed to be exceptions to the order, was the Russian scientist Mendeleev.  Todays periodic table is very similar to the one first developed by Mendeleev before all the elements were known.  In fact he was able to predict the existence of certain unknown elements because of gaps in his table.  Look carefully at the atomic masses given for the elements in the periodic table.  How many exceptions can you find to this ordering by atomic mass? 

The simple quantitative laws of chemical change allow us to calculate the quantities of elements required for a chemical reaction.  For example, lets work problems 35, 36, and 37 on page 51.
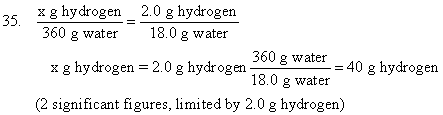
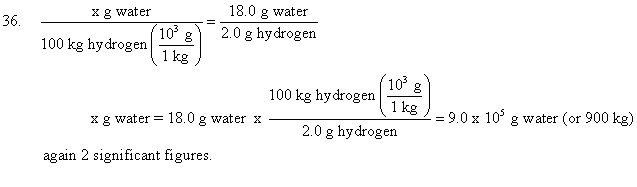