|
Chemistry 1020--Lecture 15--Notes
Review:
Chapter 4—Energy
- Definition of energy; relationship to work.
- First Law of Thermodynamics
- Mechanical energy; kinetic and potential
- Internal energy
- Heat as a form of energy
- Units of energy: Joule and calorie
- Measuring heat with a calorimeter
- Combustion reactions: writing and balancing.
- Predicting heats of reaction from bond energies
- Calculating energies per mole and energies per mass
- Comparing energy yields of fuel sources
- Interconverting energy forms
- Heat conversion to work—maximum efficiency (Thi-Tlo)/Thi
- Second Law of thermodynamics
- Entropy and randomness
- Major energy sources—historical development
- Comparison of fuel sources; advantages and disadvantages
Chapter 5—Water
- Heating curve for water;
- Specific heats of solids and liquids
- Heats of fusion and vaporization
- Unusual properties of water
- High bp and mp
- High heats of fusion and vaporization
- High specific heat
- Ice density less than liquid density
- Electronegativity
- Polarity of Molecules
- Review Lewis Dot structures
- Review molecular geometry
- Water as a solvent
- Ionic compounds
- Polyatomic ions
- Structure and nomenclature
- Covalent compounds
- Hydrogen bonding
- Amphipathic molecules—soaps and detergents
- Water sources—impurities in natural waters
- High salt
- microbial contamination
- hard water
- Water purification
- distillation
- reverse osmosis
- ion exchange
For Spring Break, you should read Chapter 6, and review Logarithms
(Appendix 3)
Introduction to Logarithms
We often deal with numbers that are very large or very small. The number
of molecules in a mole is 6.23 x 1023. The diameter of a hydrogen atom is 1.06
x 10-10 m. For this purpose, it is convenient to express numbers in exponential
form.
Often we have to deal with a range of numbers over many powers of ten,
sometimes trying to represent graphically relationships. Suppose you were a biologist
measuring the rate of growth of bacterial cells with time, and using a microscope and
appropriate dilutions of the bacterial growth solution, you collect the following data:
Time
(hours) |
Number of cells |
1 |
150 |
2 |
750 |
3 |
3750 |
4 |
1.88 x 104 |
5 |
9.38 x 104 |
6 |
4.69 x 105 |
7 |
2.34 x 106 |
8 |
1.17 x 107 |
One way of graphing this data would look as follows:
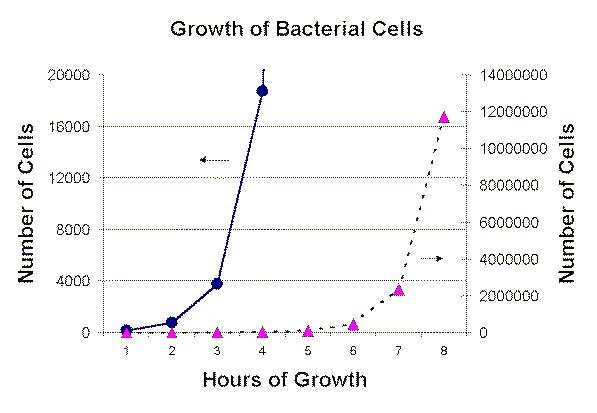
Note you cannot get all the data on one graph.
Another method is to plot the logarithm of the number of cells:
Time
(hours) |
Number of cells |
Logarithm of Number of
cells |
1 |
150 |
2.18 |
2 |
750 |
2.88 |
3 |
3750 |
3.57 |
4 |
1.88 x 104 |
4.27 |
5 |
9.38 x 104 |
4.97 |
6 |
4.69 x 105 |
5.67 |
7 |
2.34 x 106 |
6.37 |
8 |
1.17 x 107 |
7.07 |
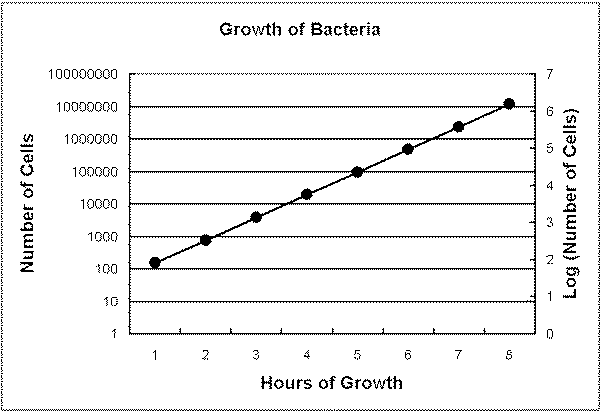
The logarithm of a number is the power of 10 equivalent to the number.
log 1 |
log 100 |
0 |
log 10 |
log 101 |
1 |
log 100 |
log 102 |
2 |
log 1000 |
log 103 |
3 |
log 10,000 |
log 104 |
4 |
log 0.1 |
log 10-1 |
-1 |
log 0.01 |
log 10-2 |
-2 |
log .001 |
log 10-3 |
-3 |
log .0001 |
log 10-4 |
-4 |
What about a number that is not an even power of 10?
For example: log 25 = log 2.5x10 = log 2.5 + log 10
The log of 2.5 can be looked up in a log table, or more easily, by
entering 2.5 on your calculator, then pushing the log button.
log 2.5 = 0.398
Note the pattern:
- log 25 = log 2.5 + log 10 = 0.398 + 1 = 1.398
- log 250 = log 2.5 + log 102 = 0.398 + 2 = 2.398
- log 2500 = log 2.5 + log 103 = 0.398 + 3 = 3.398
The 0.398 is called the mantissa of the logarithm.
The number before the decimal is called the characteristic.
| 