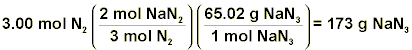|
Introduction Though based on assumptions that gas molecules do not interact with each other and occupy no volume, assumptions you will later learn to be incorrect, the Ideal Gas Law is still incredibly useful in characterizing the properties of gases. Mathematically, the Ideal Gas Law has the equation shown below, where P is the pressure in atmospheres, V is the volume in liters, n is the number of moles, T is the temperature in Kelvin, and R is a constant.
In further detail, R is know as the ideal gas constant and takes on a number of different values depending on the units used. However, for your first semester in chemistry, you will most likely only need to now that R is equal to:
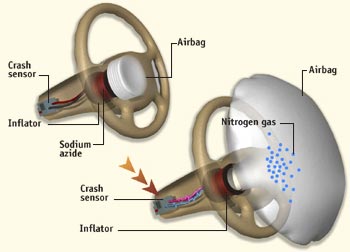
In this experiment, you will be using the Ideal Gas Law to predict the volume of gas produced from a simple chemical reaction. This reaction will be used to create a mock up of an automobile airbag. Airbags Airbags as you probably know are safety devices commonly found in most cars being produced today. The reaction used in commercial airbags depends on sodium azide (NaN3), a fairly toxic chemical. When activated, the airbag’s sodium azide rapidly undergoes a decomposition reaction generating sodium metal (Na) and nitrogen gas (N2).
In fact, it is the nitrogen gas that inflates the airbag to provide a safety cushion for the passengers in the car. Some airbags, like the one shown below can deploy in 0.015-sec for high-speed crashes and 0.025-sec for low speed crashes. All and all, the deployment and inflation processes are quicker than a blink of an eye. We guess you can say this is a pretty quick reaction.
The Reaction Since this particular laboratory is not equipped to work with chemicals as toxic as sodium azide, we will work with the similar gas producing agent sodium bicarbonate (NaHCO3). When sodium bicarbonate is allowed to react with acetic acid (CH3COOH) carbon dioxide (CO2) and two other products are formed as shown below:
The stoichiometry of this reaction is quite simple since all reactants and products are in a 1:1 molar ratio. Because the overall goal of this experiment is to design an ‘airbag’ that inflates rapidly, and fully, without wasting materials, you will need to convert molar amounts of reagents into gram and volume amounts in order to produce the precise volume of CO2 that will fill up your ‘airbag’. Stoichiometry and Manipulating the Ideal Gas Law To be able to predict the volume of the gas being produced, you will need to use the equation for the Ideal Gas Law given earlier. The variables in the Ideal Gas Law consist of volume, temperature, pressure, and the number of moles of gas. We know that our unknown in the equation is going to be the amount of gas produced. Therefore, we can rearrange the Ideal Gas Law to solve for n:
Since we know R is a constant, all we have to measure is the volume of our bag, the atmospheric pressure, and the temperature of our surroundings. For this experiment, the temperature and pressure parameters we will be using are going to be those at room conditions. Both a thermometer and a barometer, a device used to measure atmospheric pressure, can be found in the balance room. (NOTE: If you are unsure as to how to read a barometer, click here for instructions.) With the temperature and pressure taken care of, all that remains is to determine the volume of your ‘airbag’. In fact, this is the first task you are presented with in the experiment. By simply filling your 'airbag' with enough water to sufficiently fill it out and then carefully measuring that volume of water, you will be able to calculate the volume of gas you will need. The water also serves the purpose of checking the bag for leaks which would ruin your experimental results. Overall, by measuring the volume of the gas needed and inputting it, along with the room temperature and pressure, into the Ideal Gas Law, you will be able to predict the moles of gas required to fill the ‘airbag’. You can then use simple stoichiometry to calculate the mole amounts of reactants (NaHCO3 and CH3COOH) needed to produce the number of moles of CO2. Example Problem In order to further clarify the principles explored in this experiment, as well as some of the calculations required, let’s look at an example actually incorporating real data from an airbag with sodium azide. We need to find out how many grams of NaN3 are needed to completely fill a 75.0-L airbag to a pressure of 1.30-atm at 25.0°C with N2. However, before we find the mass of sodium azide required, we need to number of moles of N2.
Plugging these values into our equation as shown, we calculate that we need 3.99-mol of nitrogen gas. Now with the number of moles of N2 required, we can just use the balanced equation given at the beginning of this discussion in order to figure out the number of grams of NaN3 needed.
Therefore, we can see that in order to meet the requirements provided, we need ~173-g of sodium azide. The calculations just completed are almost identical to those you will be required to perform in this experiment!
|
 |
Gas Laws and Airbags