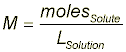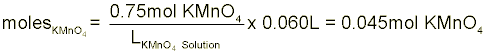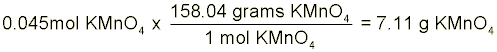Perhaps one of the most important aspects to understanding chemistry is the balanced chemical equation. En route to comprehending just how valuable a chemical equation may be, you first need to appreciate Lavoisier’s Law of Conservation of Mass. Recall from the purpose, that in its simplest terms, the law of conservation of mass states that matter can be neither created nor destroyed. Therefore, because matter is composed of atoms that are unchanged in a chemical reaction, mass must be conserved, as well as the number and types of atoms in a chemical equation.

The Reaction
The experiment you are going to conduct involves the addition of zinc metal (Zn⁰) to an acidic solution of copper (II) sulfate (CuSO₄) which is composed of copper ions (Cu⁺²) and sulfate ions (SO₄^2-). Thus, the reaction consists of the reactants, species on the left of the arrow: Zn⁰ (s), Cu²⁺ (aq), and HCl (aq), while the products of the reaction, species found to the right of the arrow, are Zn²⁺ (aq), Cu⁰ (s), Cl^- (aq), and H₂ (g). If we know the initial masses of both the solution and the metal pieces before the reaction, we can track how the masses have changed after the reaction, but we should observe that the total mass doesn't change. However, before we can proceed, we need to look at the chemical equations involved so that we can fully understand just what is taking place.

Redox
The reaction you will be running can be broken down into the two ‘mini’ net ionic reactions shown below:

In detail, both of these reactions are referred to as oxidation-reduction reactions. Over time, reactions of this sort have been coined redox reactions as they utilize two unique processes to transfer electrons. The processes to which we are referring are termed oxidation and reduction. In greater detail, oxidation involves the loss of one or more electrons from a chemical species, while reduction refers to the gain of electrons by the chemical species. These two definitions are easily remembered by the mnemonic “LEO the lion goes GER”—loses electrons, oxidized (LEO); gains electrons, reduced (GER).

In our first reaction, you can observe that the zinc metal is going from a charge of “0” to “+2”. In order to accomplish this feat, the zinc metal has to lose two electrons, or be oxidized. In the same manner, Cu²⁺ gains two electrons to form Cu⁰ and is therefore reduced. In the second ‘mini’ reaction, the hydrogen has an oxidation number of +1 on the reactants side and 0 on the product side. Is it oxidized or reduced? [Answer]

Net Reaction
These two ‘mini’ reactions are then combined, kind of like an addition problem, to form one monstrous looking equation.

In this equation, it is also important to note that in addition to solid copper (Cu⁰) being produced, a portion of zinc metal (Zn⁰) is being ionized to Zn²⁺ and hydrogen gas (H₂) is released. Click Here to see the reaction at the molecular level.

Solution Preparation
The first task in this experiment requires you to construct 25-mL of a 0.25-M solution of CuSO₄ in 3.0-M HCl. Because this is one of the first solutions you will be preparing this semester, what will follow is a tutorial-like discussion of the proper method for constructing solutions.

Instead of preparing your exact solution for you, let’s pretend that we have to make 60-mL of a 0.75-M solution of potassium permanganate (KMnO₄) in 3.0-M HCl. The first step in this process is to collect ~60-mL of the 3.0-M HCl in your 100-mL graduated cylinder. With the HCl obtained, we have to calculate just how many grams of KMnO₄ we will need to make a 0.75-M solution. In order to do this, we first have to find the number of moles in our solution and then multiply by the molecular weight of KMnO₄.

Molarity is defined as the number of moles of solute divided by the liters of solution. Note that we said liters of solution not just liters of solvent. This means that the total solution volume (including solute volume) is in the denominator.

For our solution, the solute is the potassium permanganate. Since we know the molarity of the solution is supposed to be 0.75-M and the volume is supposed to be 60-mL, we can calculate the number of moles of KMnO₄ needed:

The hardest part is now done! With the number of moles of KMnO₄ known, all we have to do is multiply by the molecular weight of potassium permanganate to get the number of grams.

We can weight out the 7.11 grams of KMnO₄ using the proper weighing technique, and then add this amount to ~50-mL of 3.0-M HCl. After stirring, we can add however much of the remaining HCl is required so that the final solution volume is 60-mL.

We will use this same type of process to produce the solution needed to perform this week's experiment.

Volume of H₂ Evolved

As stated above, the reaction we will be observing produces hydrogen gas. In order to determine that the mass of reactants and products has been conserved, we need a method by which we can collect and determine the mass of this hydrogen gas. In order to accomplish this task successfully, you will be given a side-armed Erlenmeyer flask:

and a balloon. By sealing the end of the balloon to side-arm, all of the gas released from the reaction will fill up the balloon. We can then measure the volume of the balloon by measuring its radius (r), and height (h) if necessary, and plugging them into one of the following equations:

or

Assuming that the balloon’s walls are negligible in volume, we can say that the volume of the balloon is equal to the volume of the hydrogen gas produced. Finally with this volume, you can calculate the mass of the hydrogen gas by using a form of the ideal gas law. We won't go into the details of this equation now, but simply show you how to use the equation to calculate the mass of the hydrogen gas. The Ideal gas equation is PV = nRT, where P is the room pressure which you will read from the barometer in the lab, V is the volume calculated using the equations above, n is the amount of gas in moles (what we are solving for), R is a constant with a value of 0.08206 L.atm/mol.K and T is the room temperature which is also read from the thermometer in the laboratory. Here is a practice problem:

Assume that the room temperature is 25 ^oC (298K) and the room pressure is 760 mmHg (1 atm), if the diameter of your spherical balloon is 4.2 cm, what is the mass of your hydrogen gas? [Answer]